KK's blog

每天积累多一些

0%

LeetCode 1326 Minimum Number of Taps to Open to Water a Garden

Posted on Disqus:

LeetCode



There is a one-dimensional garden on the x-axis. The garden starts at the point 0 and ends at the point n. (i.e The length of the garden is n).

There are n + 1 taps located at points [0, 1, ..., n] in the garden.

Given an integer n and an integer array ranges of length n + 1 where ranges[i] (0-indexed) means the i-th tap can water the area [i - ranges[i], i + ranges[i]] if it was open.

Return the minimum number of taps that should be open to water the whole garden, If the garden cannot be watered return -1.

Example 1:



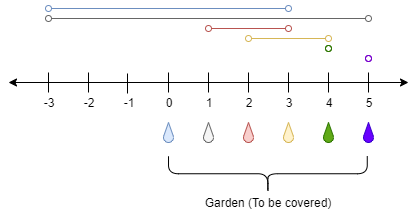
Input: n = 5, ranges = [3,4,1,1,0,0]
Output: 1
Explanation: The tap at point 0 can cover the interval [-3,3]
The tap at point 1 can cover the interval [-3,5]
The tap at point 2 can cover the interval [1,3]
The tap at point 3 can cover the interval [2,4]
The tap at point 4 can cover the interval [4,4]
The tap at point 5 can cover the interval [5,5]
Opening Only the second tap will water the whole garden [0,5]


Example 2:

Input: n = 3, ranges = [0,0,0,0]
Output: -1
Explanation: Even if you activate all the four taps you cannot water the whole garden.


Example 3:

Input: n = 7, ranges = [1,2,1,0,2,1,0,1]
Output: 3


Example 4:

Input: n = 8, ranges = [4,0,0,0,0,0,0,0,4]
Output: 2


Example 5:

Input: n = 8, ranges = [4,0,0,0,4,0,0,0,4]
Output: 1


Constraints:

1 <= n <= 10<sup>4</sup> ranges.length == n + 1
* 0 <= ranges[i] <= 100

题目大意：

用多少个水龙头覆盖整个花园

解题思路：

两个难点，此题类似于jump game，这一层某个水龙头浇到最远点的水龙头也就是这一层的水龙头，这是难点一。
难点二是跟jump game不同，这题可以往前跳，也就是如例子中，点2表示从1跳到3，因为它的范围是1. 所以要重新计算每个水龙头的起点=它的左半范围起点

解题步骤：

N/A

注意事项：

  1. 第一步转化成jump game，jump game每个数值都是长度。若左半范围起点小于等于0，所有这些水龙头归结到起点0，长度为i + ranges[i], 其余情况是ranges[i] * 2
  2. 完全用jump game的程序

Python代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def minTaps(self, n: int, ranges: List[int]) -> int:
	end, next_end, res = 0, 0, 0
	nums = [0] * len(ranges)
	for i in range(len(ranges)):
		if i - ranges[i] <= 0:
			nums[0] = max(nums[0], ranges[i] + i)
		else:
			nums[i - ranges[i]] = max(nums[i - ranges[i]], ranges[i] * 2)

	for i in range(len(nums) - 1): # remember
		if i <= end:  # -3 <= 0
			next_end = max(next_end, i + nums[i])  # 3
		if i == end:
			end = next_end
			res += 1
	return res if next_end >= len(nums) - 1 else -1

算法分析：

时间复杂度为O(n)，空间复杂度O(n)

Free mock interview