KK's blog

LeetCode 253 Meeting Rooms II

Posted on 2018-01-29 Edited on 2022-02-08 Disqus:

Given an array of meeting time intervals consisting of start and end times [[s1,e1],[s2,e2],...] (si < ei), find the minimum number of conference rooms required.

For example,
Given [[0, 30],[5, 10],[15, 20]],
return 2.

题目大意：

输入[[0, 30],[5, 10],[15, 20]]表示每个会议的开始结束时间，求最少需要多少会议室能够安排所有的会议。

最小堆解题思路：

基于merging interval题目，首先按start排序。并且merge条件是start小于上一个会议的end。

写几个例子感受一下。

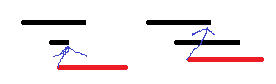
有两个重叠的会议，现在插入新的会议。是否再需要一个会议室取决于该新会议的开始时间小于这两个目前会议的终止时间的最小值。
所以思路是用End time min-heap维护目前会议End time。若新会议start time小于堆顶元素，入栈且activeMeeting++，否则循环地出栈且activeMeeting–直到
start time小于堆顶。
这过程activeMeeting的最大值即所求。
最坏情况是所有会议都重叠，复杂度为n* 2logn因为n个元素入堆出堆各一次，所以复杂度为nlogn，但会议一般不会集中，平均情况比排序法稍优。

注意事项：

Heap为结束时间的heap。
类似于递减栈模板，用开始时间与堆顶的结束时间比较（表示这些会议均已结束），若大于堆顶，连续出堆。

Python代码：

def minMeetingRooms(self, intervals: List[List[int]]) -> int:
	intervals.sort()
	heap = [] # heap for end time
	max = 0
	for i in range(len(intervals)):
		# start time of the new meeting is earlier than on-going endtime
		while heap and intervals[i][0] >= heap[0]:
			heappop(heap)
		heappush(heap, (intervals[i][1]))
		if len(heap) > max:
			max = len(heap)
	return max

算法分析：

由于输入无序，所以先要排序O(nlogn), 而循环复杂度为O(nlogk), 所以总时间复杂度为O(nlogn)，空间复杂度O(k), k为所求也就是需要的会议室数。

排序法解题思路(推荐)：

证明解与具体间隔无关，只与end time的值有关。
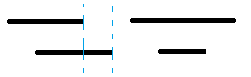
基于1和2，对end time进行排序，题解只与start-end的相对顺序有关。既然这样，我们可以把所有start，end一起排序，也就是按时间轴排列，排成一个2n大小的数组，
遇到start，activeMeeting++，遇到end，activeMeeting–。这过程activeMeeting的最大值即所求。
当然，上述方法直观，但实现起来需要建立一个class Node{value, startOrEnd}。本质上等价于对排序后的start数组和排序后的end数组进行合并排序。
合并排序的结果等价于时间轴上两个数组的统一排序。当然，不需要剩余部分的合并排序，因为这部分不会增加activeMeeting的值。

解题步骤：

排序start
排序end
合并排序，start小就activeMeeting++，否则activeMeeting–。求activeMeeting的最大值。

注意事项：

若endpoint值相同情况下，要确保第二个排序先结束点，再出发点，因为相同点不算有重复飞机

Python代码：

def minMeetingRooms(self, intervals: List[List[int]]) -> int:
	start = [(i[0], 1) for i in intervals]
	ends = [(i[1], -1) for i in intervals]
	endpoints = start + ends
	endpoints.sort()
	active_meetings, max = 0, 0
	for i in range(len(endpoints)):
		if endpoints[i][1] == 1:
			active_meetings += 1
		else:
			active_meetings -= 1
		if active_meetings > max:
			max = active_meetings
	return max

算法分析：

时间复杂度为O(nlogn)，空间复杂度O(n)。

LeetCode 572 Subtree of Another Tree

Posted on 2018-01-29 Edited on 2021-10-23 Disqus:

LeetCode 572 Subtree of Another Tree

Given two non-empty binary trees s and t, check whether tree t has exactly the same structure and node values with a subtree of s. A subtree of s is a tree consists of a node in s and all of this node’s descendants. The tree s could also be considered as a subtree of itself.

Example 1:
Given tree s:

Given tree t:

   4 
  / \
 1   2

Return true, because t has the same structure and node values with a subtree of s.

Example 2:
Given tree s:

Given tree t:

   4
  / \
 1   2

Return false.

题目大意：

给定两个非空二叉树s和t，判断t是否是s的子树。s的子树是指由s中某节点及该节点的所有子节点构成的二叉树。
特别的，s是其本身的子树。

解题思路：

这是A公司的题目。DFS解题：

s树的每一个节点与t树的根节点比较，若值相等进行下一步。
s树的某节点为根的子树和t树进行结构+值比较。

注意事项：

s=null和t=null，是子树
s和t任一为空，另一个不为空，不是子树。

Java代码：

public boolean isSubtree(TreeNode s, TreeNode t) {
	if(isSame(s, t))
		return true;
	if(t==null)
		return false;
	return s!=null && (isSubtree(s.left, t) || isSubtree(s.right, t));
}

public boolean isSame(TreeNode root, TreeNode root2){
	if(root==null && root2 == null)
		return true;
	if(root==null || root2 == null)
		return false;
	return root.val==root2.val && isSame(root.left,root2.left) && isSame(root.right, root2.right);
}

算法分析：

时间复杂度为O(nm)，空间复杂度O(1)，n和m分别为s数和t数大小。

Follow-up:

如果s是BST，怎么改进算法？
二分法先找到s的节点值等于t根节点值的节点再比较。时间复杂度为O(logn+m)。

public boolean contains(TreeNode t, TreeNode node) {
	if (node == null)
		return false;
	int result = t.compareTo(node.val);
	if (result > 0)
		return contains(t, node.right);
	else if (result < 0)
		return contains(t, node.left);
	else
		return true;
}

若BST不是严格递增 (allow duplicates)，多比较几个相等节点即可。

LeetCode 057 Insert Interval

Posted on 2018-01-29 Edited on 2021-12-29 Disqus:

LeetCode 057 Insert Interval

Given a set of non-overlapping intervals, insert a new interval into the intervals (merge if necessary).

You may assume that the intervals were initially sorted according to their start times.

Example 1:
Given intervals [1,3],[6,9], insert and merge [2,5] in as [1,5],[6,9].

Example 2:
Given [1,2],[3,5],[6,7],[8,10],[12,16], insert and merge [4,9] in as [1,2],[3,10],[12,16].

This is because the new interval [4,9] overlaps with [3,5],[6,7],[8,10].

题目大意：

对于给出的互不重叠且按照左端点排序的区间序列，将一个新的区间插入到这个序列当中（合并重叠的区间），使其仍然保持原本的性质。

Python代码：

def insert(self, intervals: List[List[int]], newInterval: List[int]) -> List[List[int]]:
	intervals.append(newInterval)
	intervals.sort(key=lambda x: x[0])
	new_interval = [intervals[0][0], intervals[0][0]]
	res = []
	for interval in intervals:
		if self.can_merge(new_interval, interval):
			new_interval = self.merge_two_intervals(new_interval, interval)
		else:
			res.append(new_interval)
			new_interval = interval
	res.append(new_interval)
	return res

def can_merge(self, interval, interval2):
	return interval[1] >= interval2[0]

def merge_two_intervals(self, interval, interval2):
	return [interval[0], max(interval[1], interval2[1])]

解题思路：

与L56题基本一致，但单元测试更加严格，加入含最大整数值的区间。

先找到start大于等于待插入区间的区间，然后待插入区间插入其前。
归结成L56题

注意事项：

先找到start大于等于待插入区间的区间，然后待插入区间插入其前。

Python代码：

def insert(self, intervals: List[List[int]], newInterval: List[int]) -> List[List[int]]:
	j = 0
	while j < len(intervals):
		if intervals[j][0] >= newInterval[0]:
			break
		j += 1
	intervals.insert(j, newInterval)

	new_interval = [intervals[0][0], intervals[0][0]]
	res = []
	for interval in intervals:
		if self.can_merge(new_interval, interval):
			new_interval = self.merge_two_intervals(new_interval, interval)
		else:
			res.append(new_interval)
			new_interval = interval
	res.append(new_interval)
	return res

def can_merge(self, interval, interval2):
	return interval[1] >= interval2[0]

def merge_two_intervals(self, interval, interval2):
	return [interval[0], max(interval[1], interval2[1])]

注意事项：

判断是否合并的API中，加入in2.start == Integer.MAX_VALUE返回false。

Java代码：

public List<Interval> insert(List<Interval> intervals, Interval newInterval) {
	int st = 0;
	for(;st<intervals.size();st++){
		if(intervals.get(st).start>=newInterval.start){
			break;
		}
	}
	intervals.add(st, newInterval);
	
	intervals.add(new Interval(Integer.MAX_VALUE, Integer.MAX_VALUE));
	List<Interval> re = new ArrayList<Interval>();
	Interval newInterval2 = null;
	for(int i=1;i<intervals.size();i++){
		if(newInterval2==null)
			newInterval2 = intervals.get(i-1);
		if(canMerge(newInterval2,intervals.get(i))){
			newInterval2 = mergeIntervals(newInterval2,intervals.get(i));
		}
		else{
			re.add(newInterval2);
			newInterval2 = null;
		}
	}
	return re;
}

算法分析：

时间复杂度为O(n)，空间复杂度O(1)，因为不用排序。

Follow-up:

先解出L56
再解此题

LeetCode 056 Merge Intervals

Posted on 2018-01-28 Edited on 2021-12-10 Disqus:

LeetCode 056 Merge Intervals

Given a collection of intervals, merge all overlapping intervals.

For example,
Given [1,3],[2,6],[8,10],[15,18],
return [1,6],[8,10],[15,18].

题目大意：

给定几个区间，要求合并重叠区间，返回结果.

解题思路：

A公司的考题。这条题难点在于判断是否合并，怎么合并，新区间合并多个区间。

按start排序。
定义API：如何合并两个区间（两情况），两个区间是否可以合并
遍历每个区间，产生新区间并将其带入到下一轮循环。这是难点，公式为新区间=新区间+输入区间[i]，这也分为两种情况，可合并和不可合并
不可合并时，前状态的新区间成为结果，公式为新区间=输入区间[i]。
若不想特别处理循环边界，可加入空区间到末尾（见Java实现，它把新区间=输入区间[i]放入了下一轮）。若不如此做，可将空区间放入开头。

注意事项：

先按左节点排序
区间的右端与另一个区间的左端一样，也算重叠，如[1,2],[2,3]。
原输入加入首节点的左边界fake区间。避免for循环的特殊处理。2. 最后一个区间的情况。
合并后生成新区间，要与下一个继续尝试合并。

Python代码：

def merge(self, intervals: List[List[int]]) -> List[List[int]]:
	intervals.sort(key=lambda x: x[0])
	new_interval = [intervals[0][0], intervals[0][0]]
	res = []
	for interval in intervals:
		if self.can_merge(new_interval, interval):
			new_interval = self.merge_two_intervals(new_interval, interval)
		else:
			res.append(new_interval)
			new_interval = interval
	res.append(new_interval)
	return res

def can_merge(self, interval, interval2):
	return interval[1] >= interval2[0]

def merge_two_intervals(self, interval, interval2):
	return [interval[0], max(interval[1], interval2[1])]

Java代码：

public List<Interval> merge(List<Interval> intervals) {
	Collections.sort(intervals, new Comparator<Interval>(){
		public int compare(Interval v1, Interval v2){
			return v1.start - v2.start;
		}
	});
	intervals.add(new Interval(Integer.MAX_VALUE, Integer.MAX_VALUE));
	List<Interval> re = new ArrayList<Interval>();
	Interval newInterval = null;
	for(int i=1;i<intervals.size();i++){
		if(newInterval==null)
			newInterval = intervals.get(i-1);
		if(canMerge(newInterval,intervals.get(i))){
			newInterval = mergeIntervals(newInterval,intervals.get(i));
		}
		else{
			re.add(newInterval);
			newInterval = null;
		}
	}
	return re;
}


//假设in与in2按start排序，所以只有两情况：
/*
 * In  -------
 * In2   ---
 * In2   -------- 
 */
public boolean canMerge(Interval in, Interval in2){
	if(in2.start == Integer.MAX_VALUE)
		return false;
	return in.end>=in2.start;
}

public Interval mergeIntervals(Interval in, Interval in2){
	return new Interval(in.start, Math.max(in.end, in2.end));
}

算法分析：

时间复杂度为O(nlogn)，空间复杂度O(1)。

LeetCode 503 Next Greater Element II

Posted on 2018-01-28 Edited on 2021-11-18 Disqus:

LeetCode 503 Next Greater Element II

Given a circular array (the next element of the last element is the first element of the array), print the Next Greater Number for every element. The Next Greater Number of a number x is the first greater number to its traversing-order next in the array, which means you could search circularly to find its next greater number. If it doesn’t exist, output -1 for this number.

Example 1:

Input: [1,2,1]
Output: [2,-1,2]
Explanation: The first 1's next greater number is 2;   
The number 2 can't find next greater number;   
The second 1's next greater number needs to search circularly, which is also 2.

Note: The length of given array won’t exceed 10000.

题目大意：

给定一个循环数组（末尾元素的下一个元素为起始元素），输出每一个元素的下一个更大的数字（Next Greater Number）。Next Greater Number是指位于某元素右侧，大于该元素，且距离最近的元素。如果不存在这样的元素，则输出-1。

注意：给定数组长度不超过10000。

解题思路：

最直接的思路是遍历每个元素，对每个元素，遍历它的后面所有元素。最差情况是递减数列，时间复杂度为O(n²)。
这题关于局部递增数组，所以考虑用递减栈。首先不考虑循环数组的情况，例如8,5,4,6,栈存入8,5,4，当6准备进栈时，5,4比6小，它们都出栈且它们的结果集为6。
循环数组其实只要将原数组复制一倍，按原算法处理，结果集取前n个元素即可。

栈不为空，准入栈元素逼出比其小的元素且赋予其结果。
该元素入栈。、
栈剩下元素的结果集赋值为-1

注意事项：

栈存储元素下标，结果集存储元素值。
栈剩下元素的结果集赋值为-1

Python代码：

def nextGreaterElements(self, nums: List[int]) -> List[int]:
	num_list = nums * 2
	result, stack = [0] * len(num_list), []
	for i in range(len(num_list)):
		while stack and num_list[i] > num_list[stack[-1]]:
			index = stack.pop()
			result[index] = num_list[i]
		stack.append(i)

	while stack:
		index = stack.pop()
		result[index] = -1
	return result[:len(nums)]

Java代码：

public int[] nextGreaterElements(int[] nums) {
	Stack s = new Stack();
	int[] nums2 = new int[nums.length*2];
	int[] re2 = new int[nums2.length];
	for(int i=0;i<nums2.length;i++){
		nums2[i] = nums[i%nums.length];
	}
	for(int i=0;i<nums2.length;i++){
		while(!s.isEmpty() && nums2[i]>nums2[(int)s.peek()]){
			int topIdx = (int)s.pop();
			re2[topIdx] = nums2[i];
		}
		s.add(i);
	}
	while(!s.isEmpty()){
		int topIdx = (int)s.pop();
		re2[topIdx] = -1;
	}
	int[] re = new int[nums.length];
	for(int i=0;i<nums.length;i++)
		re[i] = re2[i];
	return re;
}

算法分析：

时间复杂度为O(n)，空间复杂度O(n)。

有人考虑用TreeMap，
2
1 3
但TreeMap不能保留顺序，如这个TreeMap可以对应两种数组,[2,1,3], [2,3,1]并非一一对应。

Follow-up:

Given an integer array, print the Next Greater Number for every element.先从不循环数组考起。
3,8,5,4,6,7 => 8,-1,6,6,7,-1
先让其写出暴力法brute force
再优化，第0个提示是考虑用一些数据结构，第一个提示为Stack。第二个提示，给定两个stack，怎么排序一个数组。如1,4,3,2.
一个stack用于维护当前递增栈，另一个用于缓冲。过程：栈1从底到顶14，3准入，因为比4小，不能维持递增顺序，4入栈2，然后3入栈1，再把栈2所有元素入栈1。同理4,3入栈2,2入栈1。
最后如果是循环数组circular array，如果解决。
3,8,5,4,6,7 => 8,-1,6,6,7,8
第一个层次暴力法，第二层次思路从第二个提示到联系到此题解法，Meets bar。最后能实现且解决follow-up，raise bar。