KK's blog

LeetCode 2106 Maximum Fruits Harvested After at Most K Steps

Posted on 2021-12-12 Edited on 2021-12-13 Disqus:

Fruits are available at some positions on an infinite x-axis. You are given a 2D integer array fruits where fruits[i] = [positioni, amounti] depicts amounti fruits at the position positioni. fruits is already sorted by positioni in ascending order, and each positioni is unique.

You are also given an integer startPos and an integer k. Initially, you are at the position startPos. From any position, you can either walk to the left or right. It takes one step to move one unit on the x-axis, and you can walk at most k steps in total. For every position you reach, you harvest all the fruits at that position, and the fruits will disappear from that position.

Return the maximum total number of fruits you can harvest.

Example 1:

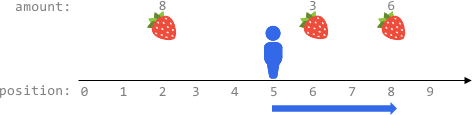
Input: fruits = [[2,8],[6,3],[8,6]], startPos = 5, k = 4
Output: 9
Explanation:
The optimal way is to:
- Move right to position 6 and harvest 3 fruits
- Move right to position 8 and harvest 6 fruits
You moved 3 steps and harvested 3 + 6 = 9 fruits in total.

Example 2:

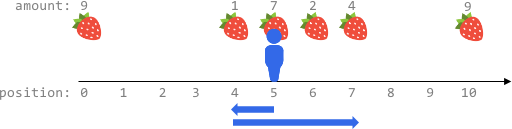
Input: fruits = [[0,9],[4,1],[5,7],[6,2],[7,4],[10,9]], startPos = 5, k = 4
Output: 14
Explanation:
You can move at most k = 4 steps, so you cannot reach position 0 nor 10.
The optimal way is to:
- Harvest the 7 fruits at the starting position 5
- Move left to position 4 and harvest 1 fruit
- Move right to position 6 and harvest 2 fruits
- Move right to position 7 and harvest 4 fruits
You moved 1 + 3 = 4 steps and harvested 7 + 1 + 2 + 4 = 14 fruits in total.

Example 3:

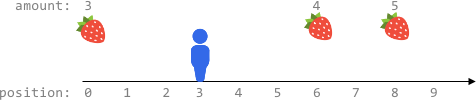
Input: fruits = [[0,3],[6,4],[8,5]], startPos = 3, k = 2
Output: 0
Explanation:
You can move at most k = 2 steps and cannot reach any position with fruits.

Constraints:

1 <= fruits.length <= 105 fruits[i].length == 2
`0 <= startPos, position_i <= 2 10⁵*position_i-1 < position_ifor anyi > 0

(**0-indexed**)
*

1 <= amount_i <= 10⁴*0 <= k <= 2 * 10⁵`

题目大意：

向左向右在规定步数内采集每一格的水果，求最大水果数

算法思路：

一开始考虑用BFS，但由于每个点可以走两次，如先往左再往右，所以不能用BFS
每个点不能走3次，因为贪婪法。所以只要计算单向路径的水果数，单向路径水果数只要计算[startPos - k - 1, startPos + k + 1]的这个区间即可
然后重复路径的范围是[0, k/2 + 1], 枚举这些值然后用presum得到单向路径水果数。

注意事项：

先判断不合法的情况sum(gas) < sum(cost)

Python代码：

def maxTotalFruits(self, fruits: List[List[int]], startPos: int, k: int) -> int:
	pos_to_fruits = collections.defaultdict(int)
	for pair in fruits:
		pos_to_fruits[pair[0]] = pair[1]
	presum = collections.defaultdict(int)
	presum[startPos - k - 1] = pos_to_fruits[startPos - k - 1]
	for i in range(startPos - k, startPos + k + 1):
		presum[i] += presum[i-1] + pos_to_fruits[i]
	res = 0
	for i in range(k//2 + 1):
		res = max(res, presum[startPos + k - i * 2] - presum[startPos - i - 1])
		res = max(res, presum[startPos + i] - presum[startPos - k + i * 2 - 1])
	return res

算法分析：

时间复杂度为O(k + n)，空间复杂度O(n + k)

LeetCode 2104 Sum of Subarray Ranges

Posted on 2021-12-12 Edited on 2021-12-13 Disqus:

LeetCode

You are given an integer array nums. The range of a subarray of nums is the difference between the largest and smallest element in the subarray.

Return the sum of all subarray ranges of nums.

A subarray is a contiguous non-empty sequence of elements within an array.

Example 1:

Input: nums = [1,2,3]
Output: 4
Explanation: The 6 subarrays of nums are the following:
[1], range = largest - smallest = 1 - 1 = 0
[2], range = 2 - 2 = 0
[3], range = 3 - 3 = 0
[1,2], range = 2 - 1 = 1
[2,3], range = 3 - 2 = 1
[1,2,3], range = 3 - 1 = 2
So the sum of all ranges is 0 + 0 + 0 + 1 + 1 + 2 = 4.

Example 2:

Input: nums = [1,3,3]
Output: 4
Explanation: The 6 subarrays of nums are the following:
[1], range = largest - smallest = 1 - 1 = 0
[3], range = 3 - 3 = 0
[3], range = 3 - 3 = 0
[1,3], range = 3 - 1 = 2
[3,3], range = 3 - 3 = 0
[1,3,3], range = 3 - 1 = 2
So the sum of all ranges is 0 + 0 + 0 + 2 + 0 + 2 = 4.

Example 3:

Input: nums = [4,-2,-3,4,1]
Output: 59
Explanation: The sum of all subarray ranges of nums is 59.

Constraints:

1 <= nums.length <= 1000 -109 <= nums[i] <= 109

题目大意：

求所有子数组的最大值最小值之差的和

Stack算法思路：

参考Leetcode 907，分别求子数组最小值的相反数，子数组的最大值，这两个值的和即为所求

注意事项：

最小值用递增栈，最大值用递减栈

Python代码：

def subArrayRanges(self, nums: List[int]) -> int:
	arr = list(nums)
	arr.insert(0, -sys.maxsize)
	arr.append(-sys.maxsize)
	stack, res, = [], 0
	for i in range(len(arr)):
		while stack and arr[i] < arr[stack[-1]]:
			prev_idx = stack.pop()
			res -= arr[prev_idx] * (prev_idx - stack[-1]) * (i - prev_idx)
		stack.append(i)

	arr = list(nums)
	arr.insert(0, sys.maxsize)
	arr.append(sys.maxsize)

	for i in range(len(arr)):
		while stack and arr[i] > arr[stack[-1]]:
			prev_idx = stack.pop()
			res += arr[prev_idx] * (prev_idx - stack[-1]) * (i - prev_idx)
		stack.append(i)
	return res

算法分析：

时间复杂度为O(n)，空间复杂度O(n)

累计和算法II解题思路：

比暴力法稍优，两重循环覆盖所有子数组[i, j]，每轮循环得到最大最小值，然后O(1)内求该区间内所有最大最小值差值和。

Python代码：

def subArrayRanges(self, nums: List[int]) -> int:
	sum = 0
	for i in range(len(nums) - 1):
		min_value, max_value = nums[i], nums[i]
		for j in range(i + 1, len(nums)):
			min_value = min(min_value, nums[j])
			max_value = max(max_value, nums[j])
			sum += max_value - min_value
	return sum

算法分析：

时间复杂度为O(n^2)，空间复杂度O(1)

LeetCode 907 Sum of Subarray Minimums

Posted on 2021-12-12 Edited on 2021-12-26 Disqus:

LeetCode

Given an array of integers arr, find the sum of min(b), where b ranges over every (contiguous) subarray of arr. Since the answer may be large, return the answer modulo 10⁹ + 7.

Example 1:

Input: arr = [3,1,2,4]
Output: 17
Explanation:
Subarrays are [3], [1], [2], [4], [3,1], [1,2], [2,4], [3,1,2], [1,2,4], [3,1,2,4].
Minimums are 3, 1, 2, 4, 1, 1, 2, 1, 1, 1.
Sum is 17.

Example 2:

Input: arr = [11,81,94,43,3]
Output: 444

Constraints:

1 <= arr.length <= 3 10⁴

1 <= arr[i] <= 3 10⁴

题目大意：

求所有子数组的最小值的和

算法思路：

求区间最值用Stack，因为是最小值，所以用递增栈
一开始考虑用类似DP，因为若知道[3, 2, 6]栈为[2, 6], 8入栈，8与每一个栈内元素计算最小值，优化是用栈内的累计和，如2和6对应的累计和而不用每个元素计算。
参考了网上算法，栈内每个元素向左向右区间内（包括自己）均是最小值，所以出栈时候进行计算即可。
如[3, 2, 8, 7, 6, 9, 10, 4]栈是[2, 6, 9, 10]对应的下标，现在4入栈，9和10出栈后，6准备出栈。
prev_idx为6的下标4， i是7，6是[8, 7, 6], [7, 6], [6]三个区间的最小值prev_idx - stack[-1] = 3个区间，
而这些区间的最小值的和还要再乘以后面的大于它的数，如[7, 6]这个区间可以和这些区间合并[7, 6], [7, 6, 9], [7, 6, 9, 10], 所以(i - prev_idx) = 3
这就是arr[prev_idx] * (prev_idx - stack[-1]) * (i - prev_idx)的精髓

注意事项：

头尾加入最小值，加入头部因为公式需要栈内的前元素，这样可以处理只有一个元素出栈的情况。尾部加入最小值因为确保所有元素都出栈。

Python代码：

def sumSubarrayMins(self, arr: List[int]) -> int:
	arr.insert(0, -sys.maxsize)
	arr.append(-sys.maxsize)
	stack, res = [], 0
	for i in range(len(arr)):
		while stack and arr[i] < arr[stack[-1]]:
			prev_idx = stack.pop()
			res += arr[prev_idx] * (prev_idx - stack[-1]) * (i - prev_idx)
			res = res % (pow(10, 9) + 7)
		stack.append(i)
	return res

算法分析：

时间复杂度为O(n)，空间复杂度O(n)

LeetCode 215 Kth Largest Element in an Array

Posted on 2021-12-11 Edited on 2021-12-13 Disqus:

LeetCode

Given an integer array nums and an integer k, return the kth largest element in the array.

Note that it is the kth largest element in the sorted order, not the kth distinct element.

Example 1:

Input: nums = [3,2,1,5,6,4], k = 2
Output: 5

Example 2:

Input: nums = [3,2,3,1,2,4,5,5,6], k = 4
Output: 4

Constraints:

1 <= k <= nums.length <= 104 -104 <= nums[i] <= 104

题目大意：

求第k大的数(1th index)

Heap算法思路：

求第k个最大也就是用最小堆(大->小)

注意事项：

N/A

Python代码：

def findKthLargest(self, nums: List[int], k: int) -> int:
	res = []  # min heap
	for i in range(len(nums)):
		if i < k:
			heapq.heappush(res, nums[i])
		elif nums[i] > res[0]:
			heapq.heapreplace(res, nums[i])
	return res[0]

算法分析：

时间复杂度为O(nlogk)，空间复杂度O(k)

Quickselect算法II解题思路：

N/A

注意事项：

递归调用仍用m，而不是跟pivot_pos相关，因为m是下标位置
partition中range用[start, end)而不是len

Python代码：

def findKthLargest(self, nums: List[int], k: int) -> int:
	m = len(nums) - k
	return self.quick_select(nums, 0, len(nums) - 1, m)

def quick_select(self, nums, start, end, m):
	if start > end:
		return -1
	pivot_pos = self.partition(nums, start, end)
	if m == pivot_pos:
		return nums[pivot_pos]
	elif m < pivot_pos:
		return self.quick_select(nums, start, pivot_pos - 1, m)
	else:
		return self.quick_select(nums, pivot_pos + 1, end, m)  # remember use m not related to pivot_pos

def partition(self, nums, start, end):
	pivot, no_smaller_index = nums[end], start
	for i in range(start, end):  # remember use start and end not len
		if nums[i] < pivot:
			nums[i], nums[no_smaller_index] = nums[no_smaller_index], nums[i]
			no_smaller_index += 1
	nums[no_smaller_index], nums[end] = nums[end], nums[no_smaller_index]
	return no_smaller_index

算法分析：

T(n) = T(n/2)+n, 时间复杂度为O(n)，空间复杂度O(1)

排序算法III解题思路：

先排序

算法分析：

时间复杂度为O(nlogn)，空间复杂度O(1)

LeetCode 022 Generate Parentheses

Posted on 2021-12-11 Edited on 2021-12-13 Disqus:

LeetCode

Given n pairs of parentheses, write a function to generate all combinations of well-formed parentheses.

Example 1:

Input: n = 3
Output: [“((()))”,”(()())”,”(())()”,”()(())”,”()()()”]

Example 2:

Input: n = 1
Output: [“()”]

Constraints:

* 1 <= n <= 8

题目大意：

产生n对括号的所有可能

算法思路：

DFS填位法，运用括号定律1：左括号数 >= 右括号数，也就是左括号剩余数 < 右括号剩余数

注意事项：

复杂度的计算

Python代码：

def generateParenthesis(self, n: int) -> List[str]:
	res = []
	self.dfs(n, n, '', res)
	return res

def dfs(self, left_paren_left, right_paren_left, path, res):
	if left_paren_left == 0 and right_paren_left == 0:
		res.append(path)
		return
	if left_paren_left > 0:
		path += '('
		self.dfs(left_paren_left - 1, right_paren_left, path, res)
		path = path[:-1]
	if right_paren_left > 0 and left_paren_left < right_paren_left:
		path += ')'
		self.dfs(left_paren_left, right_paren_left - 1, path, res)
		path = path[:-1]

算法分析：

n个括号，有2n位，时间复杂度为Catalan数O[C(n,2n)/n+1]，空间复杂度O(n)