KK's blog

LeetCode 427 Construct Quad Tree

Posted on 2022-01-04 Edited on 2022-02-02 Disqus:

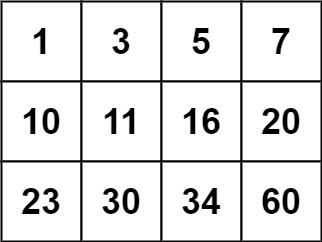
Given a n * n matrix grid of 0's and 1's only. We want to represent the grid with a Quad-Tree.

Return the root of the Quad-Tree representing the grid.

Notice that you can assign the value of a node to True or False when isLeaf is False, and both are accepted in the answer.

A Quad-Tree is a tree data structure in which each internal node has exactly four children. Besides, each node has two attributes:

val: True if the node represents a grid of 1’s or False if the node represents a grid of 0’s. isLeaf: True if the node is leaf node on the tree or False if the node has the four children.

class Node {
    public boolean val;
    public boolean isLeaf;
    public Node topLeft;
    public Node topRight;
    public Node bottomLeft;
    public Node bottomRight;
}

We can construct a Quad-Tree from a two-dimensional area using the following steps:

1. If the current grid has the same value (i.e all 1's or all 0's) set isLeaf True and set val to the value of the grid and set the four children to Null and stop.
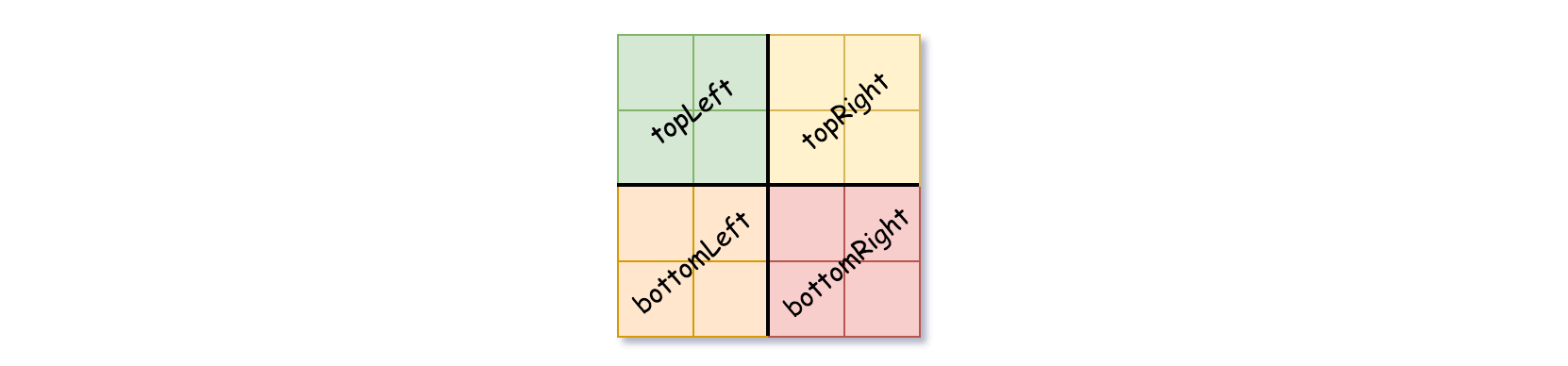
2. If the current grid has different values, set isLeaf to False and set val to any value and divide the current grid into four sub-grids as shown in the photo.
3. Recurse for each of the children with the proper sub-grid.

If you want to know more about the Quad-Tree, you can refer to the wiki.

Quad-Tree format:

The output represents the serialized format of a Quad-Tree using level order traversal, where null signifies a path terminator where no node exists below.

It is very similar to the serialization of the binary tree. The only difference is that the node is represented as a list [isLeaf, val].

If the value of isLeaf or val is True we represent it as 1 in the list [isLeaf, val] and if the value of isLeaf or val is False we represent it as 0.

Example 1:

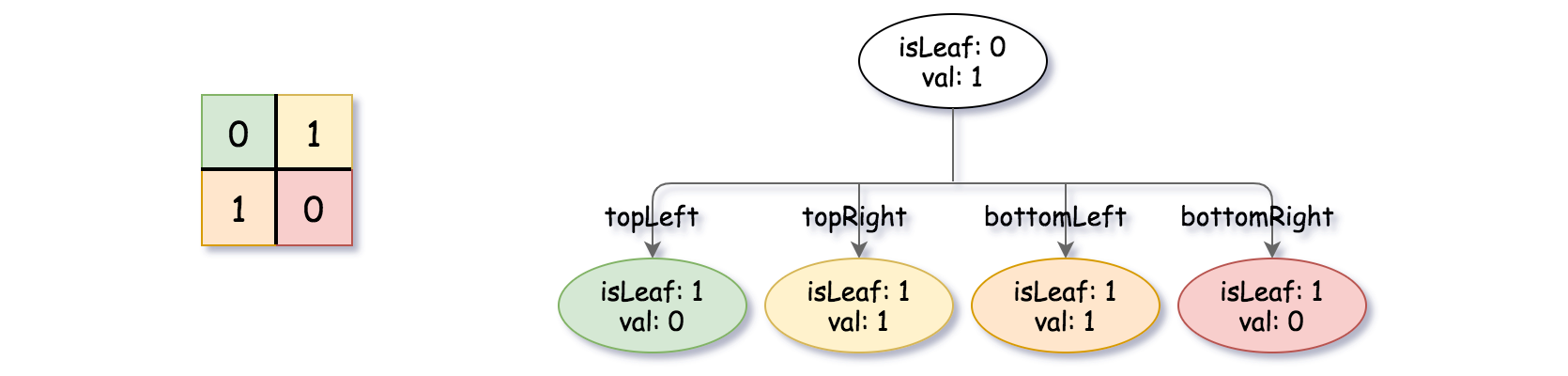
Input: grid = [[0,1],[1,0]]
Output: [[0,1],[1,0],[1,1],[1,1],[1,0]]
Explanation: The explanation of this example is shown below:
Notice that 0 represnts False and 1 represents True in the photo representing the Quad-Tree.

Example 2:

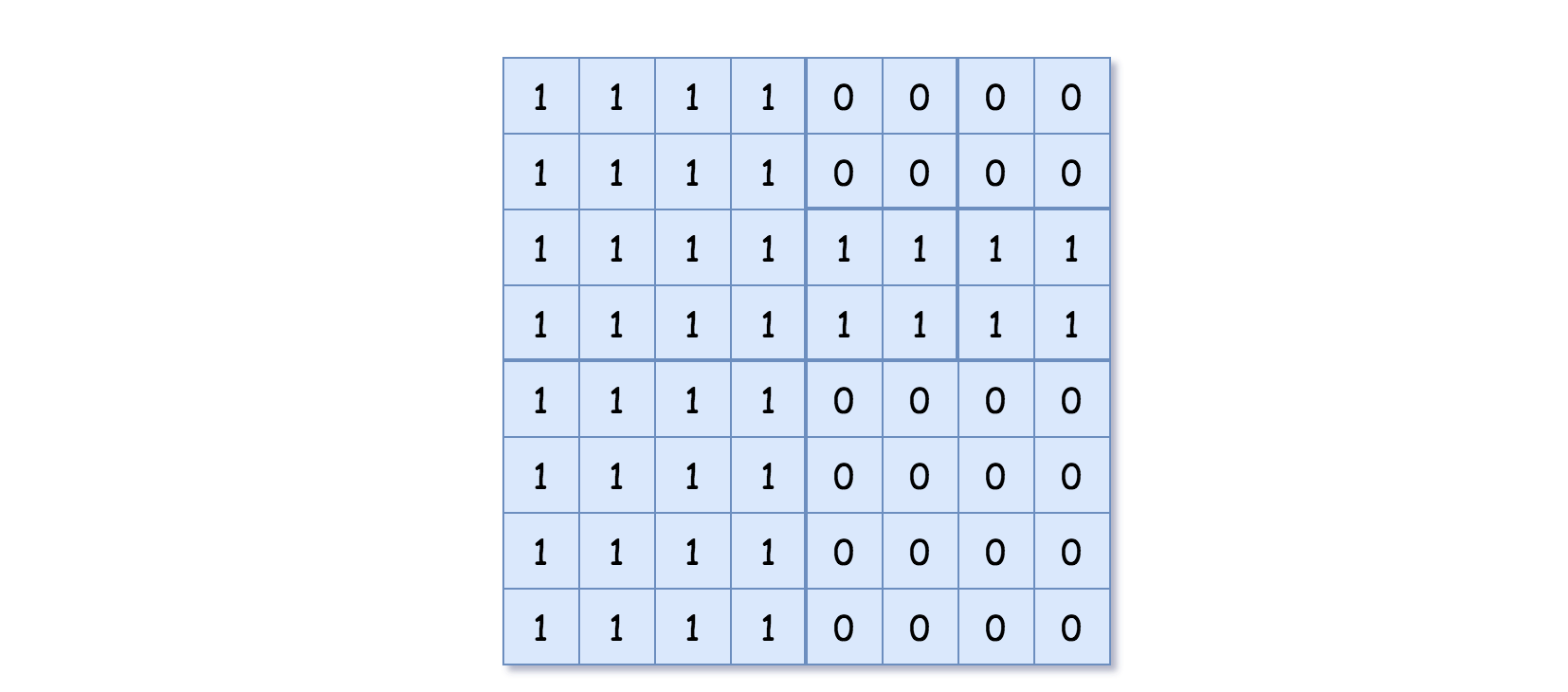
Input: grid = [[1,1,1,1,0,0,0,0],[1,1,1,1,0,0,0,0],[1,1,1,1,1,1,1,1],[1,1,1,1,1,1,1,1],[1,1,1,1,0,0,0,0],[1,1,1,1,0,0,0,0],[1,1,1,1,0,0,0,0],[1,1,1,1,0,0,0,0]]
Output: [[0,1],[1,1],[0,1],[1,1],[1,0],null,null,null,null,[1,0],[1,0],[1,1],[1,1]]
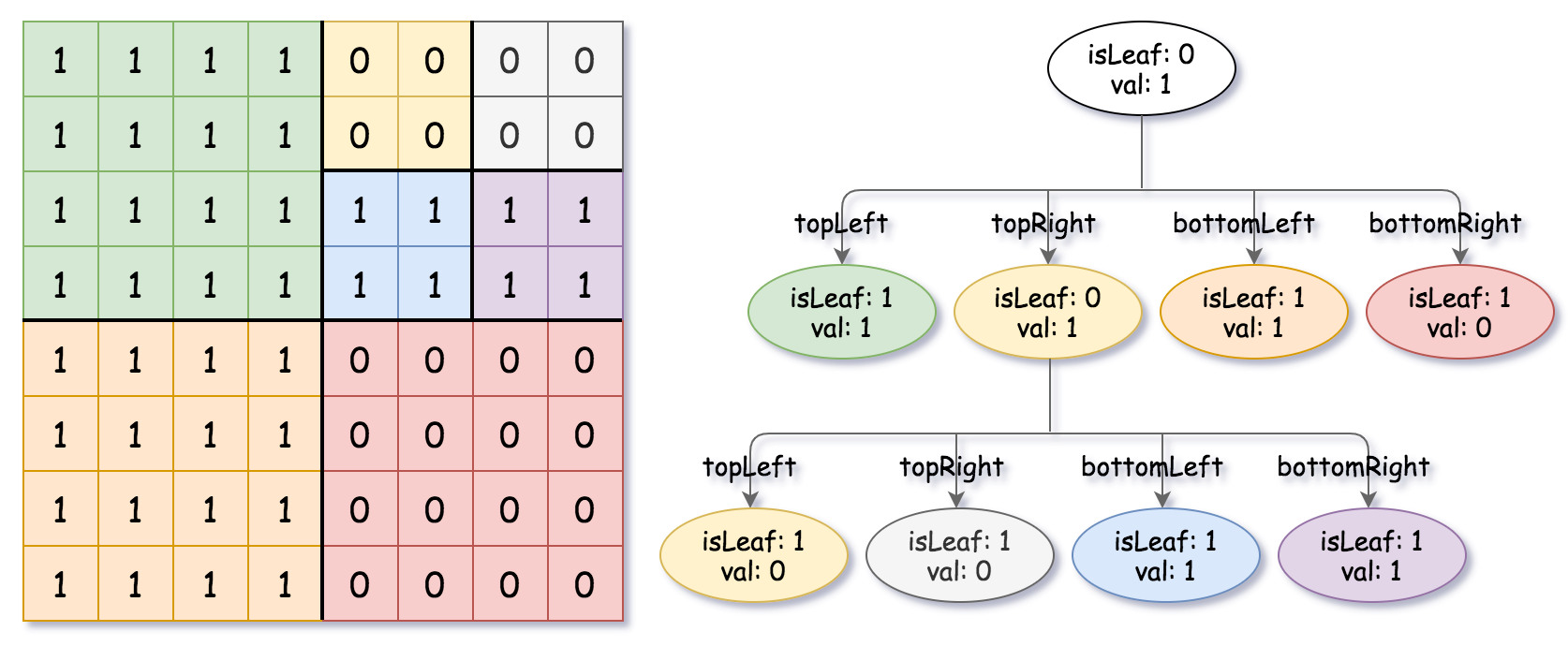
Explanation: All values in the grid are not the same. We divide the grid into four sub-grids.
The topLeft, bottomLeft and bottomRight each has the same value.
The topRight have different values so we divide it into 4 sub-grids where each has the same value.
Explanation is shown in the photo below:

Constraints:

n == grid.length == grid[i].length n == 2x where 0 <= x <= 6

题目大意：

由矩阵建四叉树。矩阵有0和1组成。按以下步骤：若子矩阵(变成为2的幂)只含1或0，生成一个叶子节点，值为该值；子矩阵含0和1混合，值为0或1(均为答案)，非叶子节点，递归四个同样大小的矩阵生成相应节点。
矩阵大小为2的幂，最小长度为1.

单格DFS算法II解题思路(推荐)：

也是DFS，但递归终止条件为长度1，也就是每个cell都是叶子节点，先递归然后再归纳，若四个儿子节点都是叶子节点且值都相等，合并为一个叶子节点。否则为非叶子节点。
此算法实现更简单，但比较难想出。上述方法思想是按照题意。

注意事项：

size = 1作为终止条件
两个条件该轮递归的节点为叶子节点，第一值相等，第二儿子节点都是叶子节点

Python代码：

def construct(self, grid: List[List[int]]) -> 'Node':
	return self.dfs(grid, 0, 0, len(grid))

def dfs(self, grid, start_x, start_y, n):
	if n == 1:
		return Node(grid[start_x][start_y], True, None, None, None, None)
	top_left = self.dfs(grid, start_x, start_y, n // 2)
	top_right = self.dfs(grid, start_x, start_y + n // 2, n // 2)
	bottom_left = self.dfs(grid, start_x + n // 2, start_y, n // 2)
	bottom_right = self.dfs(grid, start_x + n // 2, start_y + n // 2, n // 2)
	if top_left.val == top_right.val == bottom_left.val == bottom_right.val and \
			top_left.isLeaf and top_right.isLeaf and bottom_left.isLeaf and bottom_right.isLeaf: # remmember
		return Node(top_left.val, True, None, None, None, None)
	else:
		return Node(1, False, top_left, top_right, bottom_left, bottom_right)

算法分析：

时间复杂度为O(n²)，空间复杂度O(1)`

presum解题思路(不推荐)：

这是我的方法，按照定义求解，定义是递归的，所以用DFS。而统计子矩阵和用presum提高效率。但实现比较复杂

解题步骤：

N/A

注意事项：

子矩阵presum用模板
终止条件为子矩阵sum是0或n平方

Python代码：

def construct(self, grid: List[List[int]]) -> 'Node':
	presum = self.get_presum(grid)
	return self.dfs(grid, (0, 0), (len(grid) - 1, len(grid[0]) - 1), presum)

def dfs(self, grid, top_left, bottom_right, presum):
	grim_sum = self.get_grid_sum(top_left, bottom_right, presum)
	if grim_sum == 0:
		return Node(0, True, None, None, None, None)
	if grim_sum == (bottom_right[0] - top_left[0] + 1) * (bottom_right[0] - top_left[0] + 1):
		return Node(1, True, None, None, None, None)

	node = Node(1, False, None, None, None, None)
	row_mid = top_left[0] + (bottom_right[0] - top_left[0]) // 2
	col_mid = top_left[1] + (bottom_right[1] - top_left[1]) // 2
	node.topLeft = self.dfs(grid, top_left, (row_mid, col_mid), presum)
	node.topRight = self.dfs(grid, (top_left[0], col_mid + 1), (row_mid, bottom_right[1]), presum)
	node.bottomLeft = self.dfs(grid, (row_mid + 1, top_left[1]), (bottom_right[0], col_mid), presum)
	node.bottomRight = self.dfs(grid, (row_mid + 1, col_mid + 1), bottom_right, presum)
	return node

def get_grid_sum(self, top_left, bottom_right, presum):
	left = 0 if top_left[1] < 1 else presum[bottom_right[0]][top_left[1] - 1]
	top = 0 if top_left[0] < 1 else presum[top_left[0] - 1][bottom_right[1]]
	diag = 0 if top_left[0] < 1 or top_left[1] < 1 else presum[top_left[0] - 1][top_left[1] - 1]
	return presum[bottom_right[0]][bottom_right[1]] - left - top + diag

def get_presum(self, grid):
	presum = [[0 for _ in range(len(grid[0]))] for _ in range(len(grid))]
	for i in range(len(grid)):
		row_sum = 0
		for j in range(len(grid[0])):
			row_sum += grid[i][j]
			presum[i][j] = row_sum + (presum[i - 1][j] if i > 0 else 0)
	return presum

算法分析：

时间复杂度为O(n²)`，空间复杂度O(n²)

LeetCode 387 First Unique Character in a String

Posted on 2022-01-04 Disqus:

LeetCode

Given a string s, find the first non-repeating character in it and return its index. If it does not exist, return -1.

Example 1:

Input: s = “leetcode”
Output: 0

Example 2:

Input: s = “loveleetcode”
Output: 2

Example 3:

Input: s = “aabb”
Output: -1

Constraints:

1 <= s.length <= 105 s consists of only lowercase English letters.

题目大意：

求字符串中第一个唯一的字符下标

解题思路：

Easy题。先统计频率，然后再遍历一次字符串找到频率为1的字符

解题步骤：

N/A

注意事项：

Python代码：

def firstUniqChar(self, s: str) -> int:
	char_to_count = collections.Counter(s)
	for i in range(len(s)):
		if char_to_count[s[i]] == 1:
			return i
	return -1

算法分析：

时间复杂度为O(n)，空间复杂度O(1), 26个字母为常量空间

LeetCode 339 Nested List Weight Sum

Posted on 2022-01-04 Edited on 2022-02-03 Disqus:

LeetCode

You are given a nested list of integers nestedList. Each element is either an integer or a list whose elements may also be integers or other lists.

The depth of an integer is the number of lists that it is inside of. For example, the nested list [1,[2,2],[[3],2],1] has each integer’s value set to its depth.

Return the sum of each integer in nestedList multiplied by its depth.

Example 1:

Input: nestedList = [[1,1],2,[1,1]]
Output: 10
Explanation: Four 1’s at depth 2, one 2 at depth 1. 12 + 12 + 21 + 12 + 12 = 10.

Example 2:

Input: nestedList = [1,[4,[6]]]
Output: 27
Explanation: One 1 at depth 1, one 4 at depth 2, and one 6 at depth 3. 11 + 42 + 63 = 27.

Example 3:

Input: nestedList = [0]
Output: 0

Constraints:

1 <= nestedList.length <= 50 The values of the integers in the nested list is in the range [-100, 100].
The maximum *depth of any integer is less than or equal to 50.

题目大意：

求NestedInteger的和。越深，权重越高

最后计算权重解题思路(推荐)：

BFS按层遍历

Nested List题目：
LeetCode 341 Flatten Nested List Iterator Iterator - Stack
LeetCode 339 Nested List Weight Sum - BFS
LeetCode 364 Nested List Weight Sum II - BFS

解题步骤：

N/A

注意事项：

Line 9中，需要将NestedInteger展开，里面的所有的NestedInteger入列。Python中，用extend来加入list中所有元素到另一个list，而不是append
按层遍历模板中，不需要level变量，for可以达到。

Python代码：

def depthSum(self, nestedList) -> int:
	queue = collections.deque(nestedList)
	sums, max_depth, res = [], 0, 0
	while queue:
		layer_sum = 0
		for _ in range(len(queue)):
			node = queue.popleft()
			if node.isInteger():
				layer_sum += node.getInteger()
			else:
				queue.extend(node.getList()) # remember
		sums.append(layer_sum)
		max_depth += 1
	for i, n in enumerate(sums):
		res += n * (i + 1)
	return res

算法分析：

时间复杂度为O(n)，空间复杂度O(k), k为每层最多节点数 + 最大层数

每层计算权重算法II解题思路：

Python代码：

def depthSum(self, nestedList) -> int:
	queue = collections.deque(nestedList)
	res, layer = 0, 1
	while queue:
		level_sum = 0
		for _ in range(len(queue)):
			node = queue.popleft()
			if not node.isInteger():
				queue.extend(node.getList()) # remember
			else:
				level_sum += node.getInteger()
		res += level_sum * layer
		layer += 1
	return res

算法分析：

时间复杂度为O(n)，空间复杂度O(k)

LeetCode 074 Search a 2D Matrix

Posted on 2022-01-04 Edited on 2022-01-18 Disqus:

LeetCode

Write an efficient algorithm that searches for a value in an m x n matrix. This matrix has the following properties:

Integers in each row are sorted from left to right. The first integer of each row is greater than the last integer of the previous row.

Example 1:

Input: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
Output: true

Example 2:

Input: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13
Output: false

Constraints:

m == matrix.length n == matrix[i].length
1 <= m, n <= 100 -104 <= matrix[i][j], target <= 104

题目大意：

矩阵中每一行有序，下一行的首元素大于上一行的尾元素。求target是否在矩阵中

列+行搜索解题思路：

先对列做二分搜索，再对行

LeetCode 074 Search a 2D Matrix 每一行有序，下一行的首元素大于上一行的尾元素 + 找target
LeetCode 240 Search a 2D Matrix II 按行按列有序 + 找target
LeetCode 378 Kth Smallest Element in a Sorted Matrix 按行按列有序 + 找第k大
矩阵结构方面，第一道每一行都是独立，所以可以独立地按行按列做二分法
后两道，矩阵二维连续，所以解法都是类BFS，从某个点开始，然后比较它相邻的两个点。出发点不同，第二道在近似矩阵中点(右上角或左下角)，第三道在左上角出发。

解题步骤：

N/A

注意事项：

Python代码：

def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
	col = [matrix[i][0] for i in range(len(matrix))]
	row_idx = bisect.bisect(col, target) - 1
	if row_idx < 0 or row_idx >= len(matrix):
		return False
	if matrix[row_idx][0] == target:
		return True
	col_idx = bisect.bisect(matrix[row_idx], target) - 1
	if col_idx < 0 or col_idx >= len(matrix[0]):
		return False
	return True if matrix[row_idx][col_idx] == target else False

算法分析：

时间复杂度为O(logn + logm)，空间复杂度O(n), 可以写一个二分法来做列搜索，这样空间为常量。

全矩阵搜索算法II解题思路：

对矩阵的左上，右下元素作为start, end得到mid转化成(i, j)找到矩阵位置。

Java代码：

public boolean searchMatrix(int[][] matrix, int target) {
	if (matrix.length==0)
		return false;
	int lo = 0;
	int hi = matrix.length*matrix[0].length - 1;
	while (lo <= hi) {
		// Key is in a[lo..hi] or not present.
		int mid = lo + (hi - lo) / 2;
		int x = mid/matrix[0].length;
		int y = mid%matrix[0].length;
		if (target < matrix[x][y])
			hi = mid - 1;
		else if (target > matrix[x][y])
			lo = mid + 1;
		else
			return true;
	}
	return false;
}

算法分析：

时间复杂度为O(logn + logm)，空间复杂度O(1)。

LeetCode 008 String to Integer (atoi)

Posted on 2022-01-04 Edited on 2022-01-13 Disqus:

LeetCode

Implement the myAtoi(string s) function, which converts a string to a 32-bit signed integer (similar to C/C++’s atoi function).

The algorithm for myAtoi(string s) is as follows:

1. Read in and ignore any leading whitespace.
2. Check if the next character (if not already at the end of the string) is '-' or '+'. Read this character in if it is either. This determines if the final result is negative or positive respectively. Assume the result is positive if neither is present.
3. Read in next the characters until the next non-digit character or the end of the input is reached. The rest of the string is ignored.
4. Convert these digits into an integer (i.e. "123" -> 123, "0032" -> 32). If no digits were read, then the integer is 0. Change the sign as necessary (from step 2).
5. If the integer is out of the 32-bit signed integer range [-231, 231 - 1], then clamp the integer so that it remains in the range. Specifically, integers less than -231 should be clamped to -231, and integers greater than 231 - 1 should be clamped to 231 - 1.
6. Return the integer as the final result.

Note:

Only the space character ' ' is considered a whitespace character. Do not ignore any characters other than the leading whitespace or the rest of the string after the digits.

Example 1:

Input: s = “42”
Output: 42
Explanation: The underlined characters are what is read in, the caret is the current reader position.
Step 1: “42” (no characters read because there is no leading whitespace)
         ^
Step 2: “42” (no characters read because there is neither a ‘-‘ nor ‘+’)
         ^
Step 3: “42“ (“42” is read in)
           ^
The parsed integer is 42.
Since 42 is in the range [-2³¹, 2³¹ - 1], the final result is 42.

Example 2:

Input: s = “   -42”
Output: -42
Explanation:
Step 1: “-42” (leading whitespace is read and ignored)
            ^
Step 2: “   -42” (‘-‘ is read, so the result should be negative)
             ^
Step 3: “   -42“ (“42” is read in)
               ^
The parsed integer is -42.
Since -42 is in the range [-2³¹, 2³¹ - 1], the final result is -42.

Example 3:

Input: s = “4193 with words”
Output: 4193
Explanation:
Step 1: “4193 with words” (no characters read because there is no leading whitespace)
         ^
Step 2: “4193 with words” (no characters read because there is neither a ‘-‘ nor ‘+’)
         ^
Step 3: “4193 with words” (“4193” is read in; reading stops because the next character is a non-digit)
             ^
The parsed integer is 4193.
Since 4193 is in the range [-2³¹, 2³¹ - 1], the final result is 4193.

Constraints:

0 <= s.length <= 200 s consists of English letters (lower-case and upper-case), digits (0-9), ' ', '+', '-', and '.'.

题目大意：

字符串转整数

解题思路：

关键是第一位是否符号的判断，之后是ord函数的运用

解题步骤：

N/A

注意事项：

空字符或全空格返回0
[key]若有符号只能第一位是符号，连续是符号不合法返回0，如-+12, 将符号处理放在循环外
除符号外，若第一位为非数字，不合法，返回0
循环内，若出现非数字，跳出循环
计算符号，然后检查数字范围

Python代码：

def myAtoi(self, s: str) -> int:
	s = s.strip()
	if not s:
		return 0
	sign = 1
	if s[0] == '-':
		sign = -1
		s = s[1:]
	elif s[0] == '+':
		s = s[1:]
	if s and not s[0].isdigit():
		return 0
	res = 0
	for char in s:
		if char.isdigit():
			res = res * 10 + ord(char) - ord('0')
		else:
			break
	res *= sign
	if res < -pow(2, 31):
		return -pow(2, 31)
	if res > pow(2, 31) - 1:
		return pow(2, 31) - 1
	return res

算法分析：

时间复杂度为O(n)，空间复杂度O(1)