KK's blog

LeetCode

Given an m x n binary grid grid where each 1 marks the home of one friend, return the minimal total travel distance.

The total travel distance is the sum of the distances between the houses of the friends and the meeting point.

The distance is calculated using Manhattan Distance, where distance(p1, p2) = |p2.x - p1.x| + |p2.y - p1.y|.

Example 1:

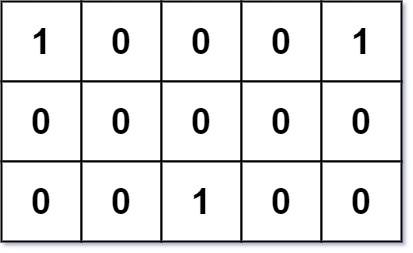
Input: grid = [[1,0,0,0,1],[0,0,0,0,0],[0,0,1,0,0]]
Output: 6
Explanation: Given three friends living at (0,0), (0,4), and (2,2).
The point (0,2) is an ideal meeting point, as the total travel distance of 2 + 2 + 2 = 6 is minimal.
So return 6.

Example 2:

Input: grid = [[1,1]]
Output: 1

Constraints:

m == grid.length n == grid[i].length
1 <= m, n <= 200 grid[i][j] is either 0 or 1.
There will be *at least two friends in the grid.

题目大意：

矩阵中1表示朋友的位置，求最佳见面位置，所有朋友到这个位置曼哈顿距离最短。

解题思路：

这是数学题也是非高频题。如果是一维，求最佳位置，是所有朋友位置的中点，也就是左边朋友和右边朋友的数量是一样。求距离也就是用相向双指针，求每对点的距离。
推广到二维，同理，x和y坐标是独立的。分别求距离即可。

解题步骤：

N/A

注意事项：

1. 用相向双指针，求每对点的距离

Python代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

def minTotalDistance(self, grid: List[List[int]]) -> int:
	x_coordinates, y_coordinates = [], []
	for i in range(len(grid)):
		for j in range(len(grid[0])):
			if grid[i][j] == 1:
				x_coordinates.append(i)
				y_coordinates.append(j)
	x_coordinates.sort()
	y_coordinates.sort()
	res = 0
	left, right = 0, len(y_coordinates) - 1
	while left < right:
		res += y_coordinates[right] - y_coordinates[left]
		left += 1
		right -= 1

	left, right = 0, len(x_coordinates) - 1
	while left < right:
		res += x_coordinates[right] - x_coordinates[left]
		left += 1
		right -= 1
	return res

算法分析：

时间复杂度为O(nlogn)，空间复杂度O(n), n为矩阵的长边大小

LeetCode

A city’s skyline is the outer contour of the silhouette formed by all the buildings in that city when viewed from a distance. Given the locations and heights of all the buildings, return the skyline formed by these buildings collectively.

The geometric information of each building is given in the array buildings where buildings[i] = [left<sub>i</sub>, right<sub>i</sub>, height<sub>i</sub>]:

left<sub>i</sub> is the x coordinate of the left edge of the i<sup>th</sup> building. right<sub>i</sub> is the x coordinate of the right edge of the i<sup>th</sup> building.
height<sub>i</sub> is the height of the i<sup>th</sup> building.

You may assume all buildings are perfect rectangles grounded on an absolutely flat surface at height 0.

The skyline should be represented as a list of “key points” sorted by their x-coordinate in the form [[x<sub>1</sub>,y<sub>1</sub>],[x<sub>2</sub>,y<sub>2</sub>],...]. Each key point is the left endpoint of some horizontal segment in the skyline except the last point in the list, which always has a y-coordinate 0 and is used to mark the skyline’s termination where the rightmost building ends. Any ground between the leftmost and rightmost buildings should be part of the skyline’s contour.

Note: There must be no consecutive horizontal lines of equal height in the output skyline. For instance, [...,[2 3],[4 5],[7 5],[11 5],[12 7],...] is not acceptable; the three lines of height 5 should be merged into one in the final output as such: [...,[2 3],[4 5],[12 7],...]

Example 1:

Input: buildings = [[2,9,10],[3,7,15],[5,12,12],[15,20,10],[19,24,8]]
Output: [[2,10],[3,15],[7,12],[12,0],[15,10],[20,8],[24,0]]
Explanation:
Figure A shows the buildings of the input.
Figure B shows the skyline formed by those buildings. The red points in figure B represent the key points in the output list.

Example 2:

Input: buildings = [[0,2,3],[2,5,3]]
Output: [[0,3],[5,0]]

Constraints: 1 <= buildings.length <= 10<sup>4</sup>
0 <= left<sub>i</sub> < right<sub>i</sub> <= 2<sup>31</sup> - 1 1 <= height<sub>i</sub> <= 2<sup>31</sup> - 1
* buildings is sorted by left<sub>i</sub> in non-decreasing order.

题目大意：

N/A

解题思路：

Heap(高度最大堆) + 端点排序法(先端点再高度逆序)
不是高频题，但思路值得学习
Heap(高度最大堆): LeetCode 253 Meeting Rooms II方法一，终点的最小堆
端点排序法(先端点再高度逆序)： LeetCode 253 Meeting Rooms II方法二
meeting room是新线段的start逼栈顶终点出堆，此题也是同样，但用高度的最大堆维护当前最高大厦，这与题意符合。

• 为什么要加入结束点?
  
  两种情况，第一种情况没有问题，但第二种情况就会漏掉第一栋大厦的结束点。原因是出堆的点没有被处理，但出堆的点可能有多个而且若没有新大厦它不能出堆，所以结束点逼它出堆。

• 为什么高度逆序?
  
  第一种情况在坐标2这个位置有两节点(2, 0, 0)第一栋大厦结束点, (2, 5, 3)第二栋大厦开始点，若不按高度排序，第一栋结束点会逼第一栋开始点出堆，产生天际线。若按高度逆序，后者先入堆，第一栋开始点出堆也不会产生天际线。类似于heapq.heapreplace先加入再删除或者LeetCode 354 Russian Doll Envelopes的排序方式

解题步骤：

N/A

注意事项：

1. 先顺序排序端点再逆序高度，因为当结束点和始点重合时，让高度大的先入堆可以确保不会产生矮的天际线，否则这些矮的天际线实际被包含在高的大厦里。
2. 结束点也要加入循环但不入堆。这样产生两点：
   1) start >= heap[0][1]要取等号，否则不能让这栋大厦结束点出堆。
   2) 结束点不入堆，因为它只用于产生结束点从而加入到结果集，它不产生高度，只有产生高度的点才会被加入到堆
3. 与前高度不同，也就是高度发生变化就入堆
4. 确保res[-1][1] != -heap[0][0]。用只有一栋大厦作为test case。
   1) 因为用到了res[-1][1]，所以res初始化加入[-float(‘inf’), 0]，第一个值不会用到所以无所谓不妨去负无穷，高度为0；
   2) 最后结果要排除这个点，取res[1:]
   3) 因为要用到heap[0][0]，也就是heap要永远有节点。初始化加入[0, float(‘inf’)]，高度为0，用于产生在地平线的点的高度，结束点为无穷大，确保不会被逼出堆。
   总结加入res中的为起始点，加入heap中的为结束点，它们高度均为0，但端点对称分别为负正无穷。

大厦题，首尾加入节点：
LeetCode 084 Largest Rectangle in Histogram
LeetCode 218 The Skyline Problem

实现上有点似：
LeetCode 239 Sliding Window Maximum 模板，计算，排除
LeetCode 218 The Skyline Problem 模板，加入，计算

Python代码：

1
2
3
4
5
6
7
8
9
10
11

def getSkyline(self, buildings: List[List[int]]) -> List[List[int]]:
	events = sorted(buildings + [[end, 0, 0] for _, end, _ in buildings], key=lambda x: (x[0], -x[2]))
	heap, res = [(0, float('inf'))], [[-float('inf'), 0]]
	for start, end, height in events:
		while heap and start >= heap[0][1]:
			heapq.heappop(heap)
		if height > 0: # don't push ends into the heap
			heapq.heappush(heap, (-height, end))
		if res[-1][1] != -heap[0][0]:
			res.append([start, -heap[0][0]])
	return res[1:]

算法分析：

时间复杂度为O(nlogn)，空间复杂度O(k), k为重合天际线个数，此复杂度跟Meeting Rooms II一致

LeetCode

Given an m x n binary matrix filled with 0‘s and 1‘s, find the largest square containing only 1‘s and return its area.

Example 1:

Input: matrix = [[“1”,”0”,”1”,”0”,”0”],[“1”,”0”,”1”,”1”,”1”],[“1”,”1”,”1”,”1”,”1”],[“1”,”0”,”0”,”1”,”0”]]
Output: 4

Example 2:

Input: matrix = [[“0”,”1”],[“1”,”0”]]
Output: 1

Example 3:

Input: matrix = [[“0”]]
Output: 0

Constraints:

m == matrix.length n == matrix[i].length
1 <= m, n <= 300 matrix[i][j] is '0' or '1'.

题目大意：

求子正方形矩阵全是1的最大面积

解题思路：

求最值且是矩阵考虑用DP，但公式比较难写。
dp[i][j]为以(i-1, j-1)为右下端点的正方形的边长
递归式：

1
2

dp[i][j] = min{dp[i-1][j-1], dp[i-1][j], dp[i][j-1]} + 1 if matrix[i][j] == 1
         = 0                                             otherwise

解题步骤：

严格遵守DP的5点注意事项

注意事项：

1. 严格遵守DP的5点注意事项。初始值是0，表示第一行或第一列的点的边长最多只能为1.
2. 输入是字符，所以比较是否1时候用字符比较

Python代码：

1
2
3
4
5
6
7
8
9
10
11

# dp[i][j] = min{dp[i-1][j-1], dp[i-1][j], dp[i][j-1]} + 1 if matrix[i][j] == 1
#          = 0                                             otherwise
def maximalSquare(self, matrix: List[List[str]]) -> int:
	dp = [[0 for _ in range(len(matrix[0]) + 1)] for _ in range(len(matrix) + 1)] # remember 0 not 1 or float(inf)
	# dp[0][0] = 0
	res = 0
	for i in range(1, len(dp)):
		for j in range(1, len(dp[0])):
			dp[i][j] = min(dp[i - 1][j], dp[i][j - 1], dp[i - 1][j - 1]) + 1 if matrix[i - 1][j - 1] == '1' else 0 # remember '1' not 1
			res = max(res, dp[i][j])
	return res * res

算法分析：

时间复杂度为O(n2)，空间复杂度O(n2)

LeetCode

Input
[“WordDictionary”,”addWord”,”addWord”,”addWord”,”search”,”search”,”search”,”search”]
[[],[“bad”],[“dad”],[“mad”],[“pad”],[“bad”],[“.ad”],[“b..”]]
Output
[null,null,null,null,false,true,true,true]

Explanation
WordDictionary wordDictionary = new WordDictionary();
wordDictionary.addWord(“bad”);
wordDictionary.addWord(“dad”);
wordDictionary.addWord(“mad”);
wordDictionary.search(“pad”); // return False
wordDictionary.search(“bad”); // return True
wordDictionary.search(“.ad”); // return True
wordDictionary.search(“b..”); // return True

题目大意：

设计一个数据结构支持加单词和查找单词。查找单词支持dot查询，表示配对任意字符

解题思路：

第一时间想到Trie，但难点在如果支持dot。一般Trie实现只支持单一单词查询，但是此题需要搜索所有可能节点。所以要将search加入TrieNode参数且转成DFS

解题步骤：

N/A

注意事项：

1. search加入TrieNode参数且转成DFS
2. 终止条件第二个用TrieNode为空而不是用is_end

Python代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

class WordDictionary(TestCases):

    def __init__(self):
        self.head = TrieNode()

    def addWord(self, word: str) -> None:
        it = self.head
        for i in range(len(word)):
            it = it.children[word[i]]
        it.is_end = True

    def search(self, word: str) -> bool:
        return self.search_one_node(word, self.head)

    def search_one_node(self, word, trie_node) -> bool:
        if not word and trie_node.is_end:
            return True
        if not word or not trie_node: # remember not trie_node
            return False
        if word[0] == '.':
            for child_node in trie_node.children.values():
                if self.search_one_node(word[1:], child_node):
                    return True
            return False
        if word[0] not in trie_node.children:
            return False
        return self.search_one_node(word[1:], trie_node.children[word[0]])

class TrieNode:

    def __init__(self):
        self.children = collections.defaultdict(TrieNode)  # {}
        self.is_end = False

算法分析：

search中不含dot时间复杂度为O(n), 含dot时间复杂度为O(26n)，空间复杂度O(1), n为搜索单词长度.

LeetCode

Input: numCourses = 2, prerequisites = [[1,0]]
Output: true
Explanation: There are a total of 2 courses to take.
To take course 1 you should have finished course 0. So it is possible.

Input: numCourses = 2, prerequisites = [[1,0],[0,1]]
Output: false
Explanation: There are a total of 2 courses to take.
To take course 1 you should have finished course 0, and to take course 0 you should also have finished course 1. So it is impossible.

题目大意：

课程有先修课要求，求是否可以完成所有课程

解题思路：

跟LeetCode 210 Course Schedule II几乎一样，此题求可否完成，那题求课程顺序。区别在于return那一句返回bool还是res

解题步骤：

N/A

注意事项：

1. Python代码：

   1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

   def canFinish(self, numCourses: int, prerequisites: List[List[int]]) -> bool: in_degree = [0] * numCourses graph = [[] for _ in range(numCourses)] for li in prerequisites: in_degree[li[0]] += 1 graph[li[1]].append(li[0]) queue = collections.deque([i for i in range(len(in_degree)) if in_degree[i] == 0]) res = [] while queue: node = queue.popleft() res.append(node) for neighbor in graph[node]: in_degree[neighbor] -= 1 if in_degree[neighbor] == 0: queue.append(neighbor) return numCourses == len(res)

算法分析：

时间复杂度为O(n)，空间复杂度O(n)