LeetCode 1937 Maximum Number of Points with Cost

LeetCode

You are given an m x n integer matrix points (0-indexed). Starting with 0 points, you want to maximize the number of points you can get from the matrix.

To gain points, you must pick one cell in each row. Picking the cell at coordinates (r, c) will add points[r][c] to your score.

However, you will lose points if you pick a cell too far from the cell that you picked in the previous row. For every two adjacent rows r and r + 1 (where 0 <= r < m - 1), picking cells at coordinates (r, c1) and (r + 1, c2) will subtract abs(c1 - c2) from your score.

Return the maximum number of points you can achieve.

abs(x) is defined as:

x for x >= 0. -x for x < 0.

Example 1:

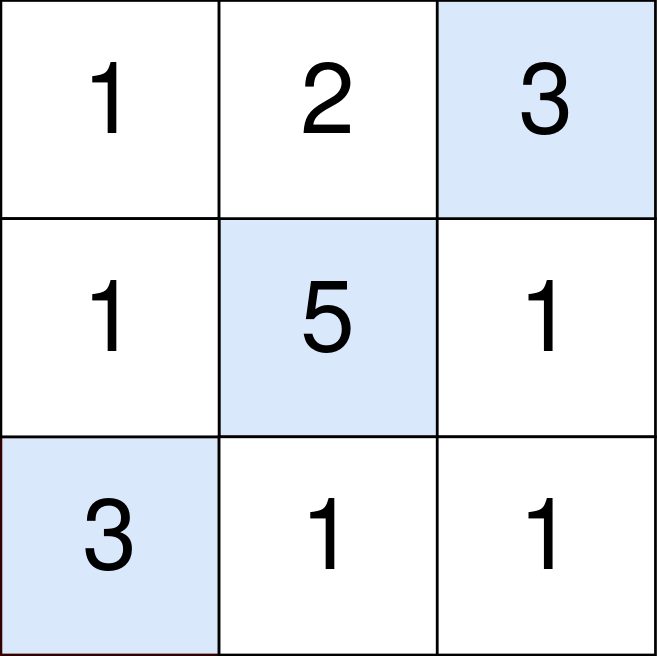
Input: points = [[1,2,3],[1,5,1],[3,1,1]]
Output: 9
Explanation:
The blue cells denote the optimal cells to pick, which have coordinates (0, 2), (1, 1), and (2, 0).
You add 3 + 5 + 3 = 11 to your score.
However, you must subtract abs(2 - 1) + abs(1 - 0) = 2 from your score.
Your final score is 11 - 2 = 9.

Example 2:

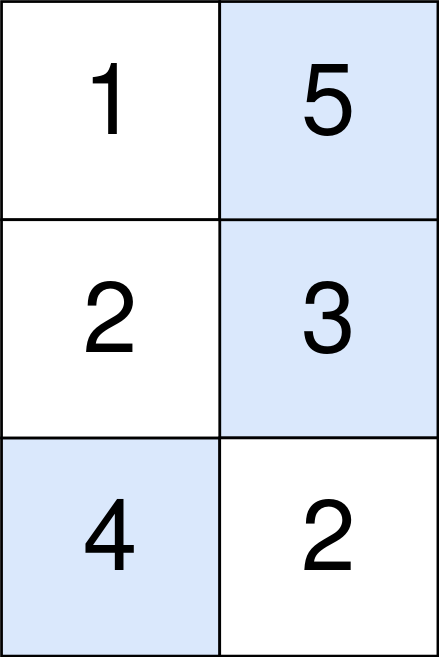
Input: points = [[1,5],[2,3],[4,2]]
Output: 11
Explanation:
The blue cells denote the optimal cells to pick, which have coordinates (0, 1), (1, 1), and (2, 0).
You add 5 + 3 + 4 = 12 to your score.
However, you must subtract abs(1 - 1) + abs(1 - 0) = 1 from your score.
Your final score is 12 - 1 = 11.

Constraints:

m == points.length n == points[r].length
1 <= m, n <= 105 1 <= m * n <= 105
* 0 <= points[r][c] <= 105

题目大意：

矩阵中含点数，每行取一个cell上的点数，但若两行之间的cell的列不同，要扣去列下标差，求最大点数

优化DP解题思路(推荐)：

求数值的最大值，容易想到用DP，dp[i][j]定义为每个cell的累计最大点数，递归式为

1	dp[i][j] = max(dp[i - 1][k] - abs(j - k)) + points[i][j], k = 0..len(dp[0])

复杂度为n立方。

如果没有扣除的规则，其实就是找上一行的最大值，但要考虑下标，考虑怎么移除这个限制，若将上一个某个cell搬到跟目前列，就是dp[i - 1][k] - (j - k), 所以可以提前计算，
而且有绝对值，所以类似于LeetCode 042 Trapping Rain Water拆分为向左向右最大值：
left[i]是该行第i个cell，上一行在该列左边的cell的累计最大点数(已扣除)，同理
right[i]是该行第i个cell，上一行在该列右边的cell的累计最大点数(已扣除)

最后，上一行的最大值只能在左边或右边

1	dp[i][j] = max(left[j], right[j]) + points[i][j], k = 0..len(dp[0])

解题步骤：

N/A

注意事项：

left[j], right[j]的引入

Python代码：

def maxPoints(self, points: List[List[int]]) -> int:
	m, n = len(points), len(points[0])
	dp = [[0 for _ in range(n)] for _ in range(m)]
	for j in range(n):
		dp[0][j] = points[0][j]
	for i in range(1, m):
		left, right = [0] * n, [0] * n
		left[0], right[-1] = dp[i - 1][0], dp[i - 1][-1]
		for j in range(1, n):
			left[j] = max(dp[i - 1][j], left[j - 1] - 1)
		for j in range(n - 2, -1, -1):
			right[j] = max(dp[i - 1][j], right[j + 1] - 1)
		for j in range(n):
			dp[i][j] = points[i][j] + max(left[j], right[j])
	return max(dp[-1])

算法分析：

时间复杂度为O(n²)，空间复杂度O(n²)

暴力DP算法II解题思路(不推荐)：

Python代码：

def maxPoints2(self, points: List[List[int]]) -> int:
	dp = [[0 for _ in range(len(points[0]))] for _ in range(len(points))]
	for j in range(len(dp[0])):
		dp[0][j] = points[0][j]
	for i in range(1, len(dp)):
		for j in range(len(dp[0])):
			for k in range(len(dp[0])):
				dp[i][j] = max(dp[i][j], dp[i - 1][k] + points[i][j] - abs(j - k))
	return max(dp[-1])

算法分析：

时间复杂度为O(n³)，空间复杂度O(n²)