KK's blog

每天积累多一些

0%

LeetCode 351 Android Unlock Patterns

Posted on Disqus:

LeetCode



Android devices have a special lock screen with a 3 x 3 grid of dots. Users can set an “unlock pattern” by connecting the dots in a specific sequence, forming a series of joined line segments where each segment’s endpoints are two consecutive dots in the sequence. A sequence of k dots is a valid unlock pattern if both of the following are true:

All the dots in the sequence are distinct. If the line segment connecting two consecutive dots in the sequence passes through the center of any other dot, the other dot must have previously appeared in the sequence. No jumps through the center non-selected dots are allowed.
For example, connecting dots 2 and 9 without dots 5 or 6 appearing beforehand is valid because the line from dot 2 to dot 9 does not pass through the center of either dot 5 or 6. However, connecting dots 1 and 3 without dot 2 appearing beforehand is invalid because the line from dot 1 to dot 3 passes through the center of dot 2.

Here are some example valid and invalid unlock patterns:



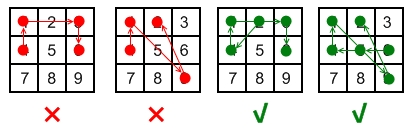
The 1st pattern [4,1,3,6] is invalid because the line connecting dots 1 and 3 pass through dot 2, but dot 2 did not previously appear in the sequence. The 2nd pattern [4,1,9,2] is invalid because the line connecting dots 1 and 9 pass through dot 5, but dot 5 did not previously appear in the sequence.
The 3rd pattern [2,4,1,3,6] is valid because it follows the conditions. The line connecting dots 1 and 3 meets the condition because dot 2 previously appeared in the sequence. The 4th pattern [6,5,4,1,9,2] is valid because it follows the conditions. The line connecting dots 1 and 9 meets the condition because dot 5 previously appeared in the sequence.

Given two integers m and n, return the number of unique and valid unlock patterns of the Android grid lock screen that consist of at least m keys and at most n keys.

Two unlock patterns are considered unique if there is a dot in one sequence that is not in the other, or the order of the dots is different.

Example 1:

Input: m = 1, n = 1
Output: 9


Example 2:

Input: m = 1, n = 2
Output: 65


Constraints:

* 1 <= m, n <= 9

题目大意：

安卓开屏密码解锁种数。给定m, n是安卓的密码长度范围，求这个范围内的解码种数。1可以跳到2和4, 5, 6, 8(斜线没有通过其他数字)，但不能跳到3, 7, 9因为前提条件是这条线通过的数如2, 4, 5必须已经用过了。

解题思路：

此题属于填位法，带条件的，条件在于map中，类似于LeetCode 248 Strobogrammatic Number III
难点是理解jump keys，有16种

1
2
3
4
5
skip[1][3] = skip[3][1] = 2;
skip[1][7] = skip[7][1] = 4;
skip[3][9] = skip[9][3] = 6;
skip[7][9] = skip[9][7] = 8;
skip[1][9] = skip[9][1] = skip[2][8] = skip[8][2] = skip[3][7] = skip[7][3] = skip[4][6] = skip[6][4] = 5;

解题步骤：

用DFS模板: def dfs(self, graph, start, visited, res), start = num

注意事项：

  1. Line 9有return，所以要去掉刚加入的visited的num

Python代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
JUMP_KEYS = {(1,3):2, (1,7):4, (1,9):5, (2,8):5, (3,7):5, (3,1):2, (3,9):6, (4,6):5, (6,4):5, (7,1):4, (7,3):5, (7,9):8, (8,2):5, (9,7):8, (9,3):6, (9,1):5}
class Solution(TestCases):

    def dfs(self, num, m, n, visited):
        if num in visited:
            return 0
        visited.add(num)
        if len(visited) == n:
            visited.remove(num) # remember
            return 1
        res = 0
        if len(visited) >= m:
            res += 1
        for next_num in range(1, 10):
            if (num, next_num) in JUMP_KEYS and JUMP_KEYS[(num, next_num)] not in visited:
                continue
            res += self.dfs(next_num, m, n, visited)
        visited.remove(num)
        return res

算法分析：

时间复杂度为O(1)，空间复杂度O(1), 因为最多是9乘以8乘以7…

Free mock interview