LeetCode 1761 Minimum Degree of a Connected Trio in a Graph

LeetCode

<div>

You are given an undirected graph. You are given an integer n which is the number of nodes in the graph and an array edges, where each edges[i] = [u<sub>i</sub>, v<sub>i</sub>] indicates that there is an undirected edge between u<sub>i</sub> and v<sub>i</sub>.

A connected trio is a set of three nodes where there is an edge between every pair of them.

The degree of a connected trio is the number of edges where one endpoint is in the trio, and the other is not.

Return the minimum degree of a connected trio in the graph, or -1 if the graph has no connected trios.

Example 1:

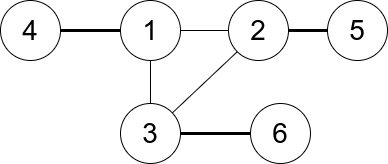
<pre>Input: n = 6, edges = [[1,2],[1,3],[3,2],[4,1],[5,2],[3,6]] Output: 3 Explanation: There is exactly one trio, which is [1,2,3]. The edges that form its degree are bolded in the figure above. </pre>

Example 2:

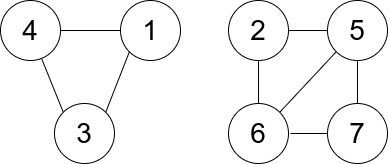
<pre>Input: n = 7, edges = [[1,3],[4,1],[4,3],[2,5],[5,6],[6,7],[7,5],[2,6]] Output: 0 Explanation: There are exactly three trios:

1. [1,4,3] with degree 0.
2. [2,5,6] with degree 2.
3. [5,6,7] with degree 2. </pre>

Constraints:

• 2 <= n <= 400
• edges[i].length == 2
• 1 <= edges.length <= n * (n-1) / 2
• 1 <= u<sub>i</sub>, v<sub>i</sub> <= n
• u<sub>i</sub> != v<sub>i</sub>
• There are no repeated edges.

</div>

题目大意：

给定一个图，trio是三个节点直接互相相连，而度数表示连着trio的边的个数

解题思路：

根据定义，找出所有三个节点的组合，判断是否trio，然后根据trio的每个节点的度数总和 - 6即为所求
遍历所有三个节点组合时，会重复了两次。所以一个优化是，先按度数排序节点，若节点度数大于等于最小度数除以3，跳出循环。因为这个最小度数的节点已经大于等于3，trio里其他两个度数比它大的节点的度数更加会大于最小度数除以3，这样总度数肯定大于此时的最小度数

解题步骤：

N/A

注意事项：

1. 根据定义，找出所有三个节点的组合u -> v, v -> w, w是否在u中，判断是否trio。先按度数排序节点，若节点度数大于等于最小度数除以3，跳出循环
2. 邻接图用set，因为Line 13查找w是否在u中可以提高效率
3. min_degree / 3不是// 3

Python代码：

def minTrioDegree(self, n: int, edges: List[List[int]]) -> int:
	graph = collections.defaultdict(set) # use set coz if w in graph[u]
	for u, v in edges:
		graph[u].add(v)
		graph[v].add(u)

	min_degree = float('inf')
	for u in sorted(range(1, n + 1), key=lambda x: len(graph[x])):
		if len(graph[u]) >= min_degree / 3: # remember / 3 not // 3
			break
		for v in graph[u]:
			for w in graph[v]:
				if w in graph[u]:
					min_degree = min(min_degree, len(graph[u]) + len(graph[v]) + len(graph[w]))
	return min_degree - 6 if min_degree != float('inf') else -1

算法分析：

时间复杂度为<code>O(n³)</code>，空间复杂度<code>O(n²)</code>