KK's blog

每天积累多一些

0%

LeetCode 785 Is Graph Bipartite?

Posted on Disqus:

LeetCode



There is an undirected graph with n nodes, where each node is numbered between 0 and n - 1. You are given a 2D array graph, where graph[u] is an array of nodes that node u is adjacent to. More formally, for each v in graph[u], there is an undirected edge between node u and node v. The graph has the following properties:

There are no self-edges (graph[u] does not contain u). There are no parallel edges (graph[u] does not contain duplicate values).
If v is in graph[u], then u is in graph[v] (the graph is undirected). The graph may not be connected, meaning there may be two nodes u and v such that there is no path between them.

A graph is bipartite if the nodes can be partitioned into two independent sets A and B such that every edge in the graph connects a node in set A and a node in set B.

Return true if and only if it is bipartite.

Example 1:



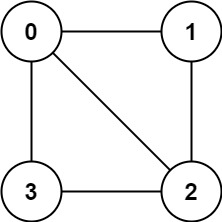
Input: graph = [[1,2,3],[0,2],[0,1,3],[0,2]]
Output: false
Explanation: There is no way to partition the nodes into two independent sets such that every edge connects a node in one and a node in the other.


Example 2:



Input: graph = [[1,3],[0,2],[1,3],[0,2]]
Output: true
Explanation: We can partition the nodes into two sets: {0, 2} and {1, 3}.


Constraints:

graph.length == n 1 <= n <= 100
0 <= graph[u].length < n 0 <= graph[u][i] <= n - 1
graph[u] does not contain u. All the values of graph[u] are unique.
* If graph[u] contains v, then graph[v] contains u.

题目大意：

无向图中是否存在一个划分，将节点分为两集合，任何一条边都连接着两个集合，也就是不存在一条边在单一集合内。

解题思路：

图上色法。两种颜色，将节点上色0，儿子上色1，若某个节点已经上的色和将要上的色矛盾（来自的路径不同），即不合法

解题步骤：

N/A

注意事项：

  1. 图上色法。两种颜色，将节点上色0，儿子上色1，若某个节点已经上的色和将要上的色矛盾（来自的路径不同），即不合法
  2. 题意表示，图可能是有几个连通图，所以要从每个节点做BFS，除非节点已访问过， Line 4. node_to_color作为visited的功能
  3. return True在两个函数中要写，否则返回None

Python代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
def isBipartite(self, graph: List[List[int]]) -> bool:
	node_to_color = collections.defaultdict(int)
	for i in range(len(graph)):
		if i in node_to_color: # disconnected nodes
			continue
		node_to_color[i] = 0
		if not self.bfs(graph, i, node_to_color):
			return False
	return True

def bfs(self, graph, n, node_to_color):
	queue = collections.deque([n])
	while queue:
		node = queue.popleft()
		for neighbor in graph[node]:
			if neighbor in node_to_color and node_to_color[neighbor] != 1 - node_to_color[node]:
				return False
			if neighbor in node_to_color:
				continue
			queue.append(neighbor)
			node_to_color[neighbor] = 1 - node_to_color[node]
	return True

算法分析：

时间复杂度为O(V + E)，空间复杂度O(V + E)

Free mock interview