LeetCode 317 Shortest Distance from All Buildings

LeetCode

You are given an m x n grid grid of values 0, 1, or 2, where:

each 0 marks an empty land that you can pass by freely, each 1 marks a building that you cannot pass through, and
each 2 marks an obstacle that you cannot pass through.

You want to build a house on an empty land that reaches all buildings in the shortest total travel distance. You can only move up, down, left, and right.

Return the shortest travel distance for such a house. If it is not possible to build such a house according to the above rules, return -1.

The total travel distance is the sum of the distances between the houses of the friends and the meeting point.

The distance is calculated using Manhattan Distance, where distance(p1, p2) = |p2.x - p1.x| + |p2.y - p1.y|.

Example 1:

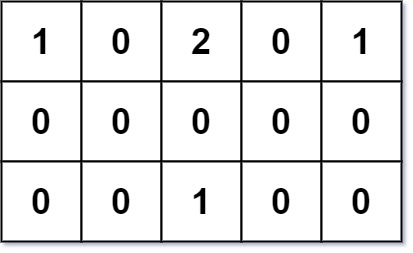
Input: grid = [[1,0,2,0,1],[0,0,0,0,0],[0,0,1,0,0]]
Output: 7
Explanation: Given three buildings at (0,0), (0,4), (2,2), and an obstacle at (0,2).
The point (1,2) is an ideal empty land to build a house, as the total travel distance of 3+3+1=7 is minimal.
So return 7.

Example 2:

Input: grid = [[1,0]]
Output: 1

Example 3:

Input: grid = [[1]]
Output: -1

Constraints: m == grid.length
n == grid[i].length 1 <= m, n <= 50
grid[i][j] is either 0, 1, or 2. There will be at least one building in the grid.

题目大意：

找到所有大厦最短距离的点，这个点不能是大厦也不能是障碍

解题思路：

一开始觉得类似于LeetCode 296 Best Meeting Point，但由于有障碍，所以不能用贪婪法。最值考虑用BFS。属于对所有节点BFS。类似于LeetCode 200 Number of Islands，
从每一栋大厦开始做BFS，计算每个点到此大厦距离。然后对累计到这个点的总距离矩阵dis中。最后求距离矩阵的最小值。

此题难点在于-1的情况，也就是一个点不能到达其中一个building或者是这个building不能到达的点。所以要再用一个矩阵house_count来记录每一个点能到达的大厦数。

解题步骤：

N/A

注意事项：

1. -1的情况，用一个矩阵house_count来记录每一个点能到达的大厦数。
2. 用常数记录矩阵长和宽，不用x >= len(grid) or y >= len(grid[0]), 否则会TLE

Python代码：

OFFSETS = [(-1, 0), (1, 0), (0, -1), (0, 1)]
def shortestDistance(self, grid: List[List[int]]) -> int:
	dis = [[0 for _ in range(len(grid[0]))] for _ in range(len(grid))]
	house_count = [[0 for _ in range(len(grid[0]))] for _ in range(len(grid))]
	total_houses = 0
	for i in range(len(grid)):
		for j in range(len(grid[0])):
			if grid[i][j] == 1:
				self.bfs(grid, i, j, dis, house_count)
				total_houses += 1
	min_dis = float('inf') # remember
	for i in range(len(dis)):
		for j in range(len(dis[0])):
			if dis[i][j] > 0 and house_count[i][j] == total_houses:
				min_dis = min(min_dis, dis[i][j])
	return -1 if min_dis == float('inf') else min_dis # remember

def bfs(self, grid, start_x, start_y, dis, house_count):
	h = len(grid)
	w = len(grid[0]) # remember otherwise TLE
	queue = collections.deque([(start_x, start_y, 0)])
	visited = [[False for _ in range(len(grid[0]))] for _ in range(len(grid))]
	visited[start_x][start_y] = True
	while queue:
		node = queue.popleft()
		for _dx, _dy in OFFSETS:
			x, y = node[0] + _dx, node[1] + _dy
			if x < 0 or x >= h or y < 0 or y >= w or grid[x][y] != 0 or visited[x][y]:
				continue
			queue.append((x, y, node[2] + 1))
			visited[x][y] = True
			dis[x][y] += node[2] + 1
			house_count[x][y] += 1

算法分析：

时间复杂度为O(nm * nm)，空间复杂度O(nm)