LeetCode 240 Search a 2D Matrix II

LeetCode

Write an efficient algorithm that searches for a target value in an m x n integer matrix. The matrix has the following properties:

Integers in each row are sorted in ascending from left to right. Integers in each column are sorted in ascending from top to bottom.

Example 1:

Input: matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
Output: true

Example 2:

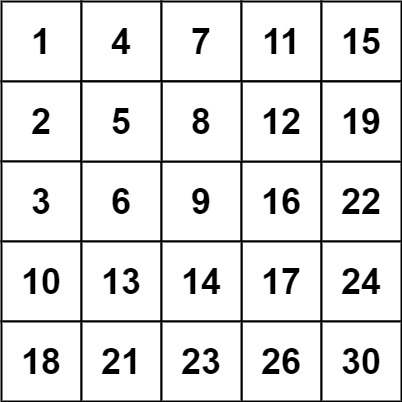
Input: matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20
Output: false

Constraints:

m == matrix.length n == matrix[i].length
1 <= n, m <= 300 -10<sup>9</sup> <= matrix[i][j] <= 10<sup>9</sup>
All the integers in each row are sorted in ascending order. All the integers in each column are sorted in ascending order.
* -10<sup>9</sup> <= target <= 10<sup>9</sup>

题目大意：

矩阵按行按列有序，求是否存在target

解题思路：

矩阵有序题有3道：
LeetCode 074 Search a 2D Matrix 每一行有序，下一行的首元素大于上一行的尾元素 + 找target
LeetCode 240 Search a 2D Matrix II 按行按列有序 + 找target
LeetCode 378 Kth Smallest Element in a Sorted Matrix 按行按列有序 + 找第k大
矩阵结构方面，第一道每一行都是独立，所以可以独立地按行按列做二分法
后两道，矩阵二维连续，所以解法都是类BFS，从某个点开始，然后比较它相邻的两个点。出发点不同，第二道在近似矩阵中点(右上角或左下角)，第三道在左上角出发。

解题步骤：

N/A

注意事项：

1. 从右上角出发，比较左和下节点。

Python代码：

def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
	i, j = 0, len(matrix[0]) - 1
	while i < len(matrix) and j >= 0:
		if matrix[i][j] == target:
			return True
		if target < matrix[i][j]:
			j -= 1
		else:
			i += 1
	return False

算法分析：

时间复杂度为O(n + m)，空间复杂度O(1)