LeetCode 218 The Skyline Problem

LeetCode

A city’s skyline is the outer contour of the silhouette formed by all the buildings in that city when viewed from a distance. Given the locations and heights of all the buildings, return the skyline formed by these buildings collectively.

The geometric information of each building is given in the array buildings where buildings[i] = [left<sub>i</sub>, right<sub>i</sub>, height<sub>i</sub>]:

left<sub>i</sub> is the x coordinate of the left edge of the i<sup>th</sup> building. right<sub>i</sub> is the x coordinate of the right edge of the i<sup>th</sup> building.
height<sub>i</sub> is the height of the i<sup>th</sup> building.

You may assume all buildings are perfect rectangles grounded on an absolutely flat surface at height 0.

The skyline should be represented as a list of “key points” sorted by their x-coordinate in the form [[x<sub>1</sub>,y<sub>1</sub>],[x<sub>2</sub>,y<sub>2</sub>],...]. Each key point is the left endpoint of some horizontal segment in the skyline except the last point in the list, which always has a y-coordinate 0 and is used to mark the skyline’s termination where the rightmost building ends. Any ground between the leftmost and rightmost buildings should be part of the skyline’s contour.

Note: There must be no consecutive horizontal lines of equal height in the output skyline. For instance, [...,[2 3],[4 5],[7 5],[11 5],[12 7],...] is not acceptable; the three lines of height 5 should be merged into one in the final output as such: [...,[2 3],[4 5],[12 7],...]

Example 1:

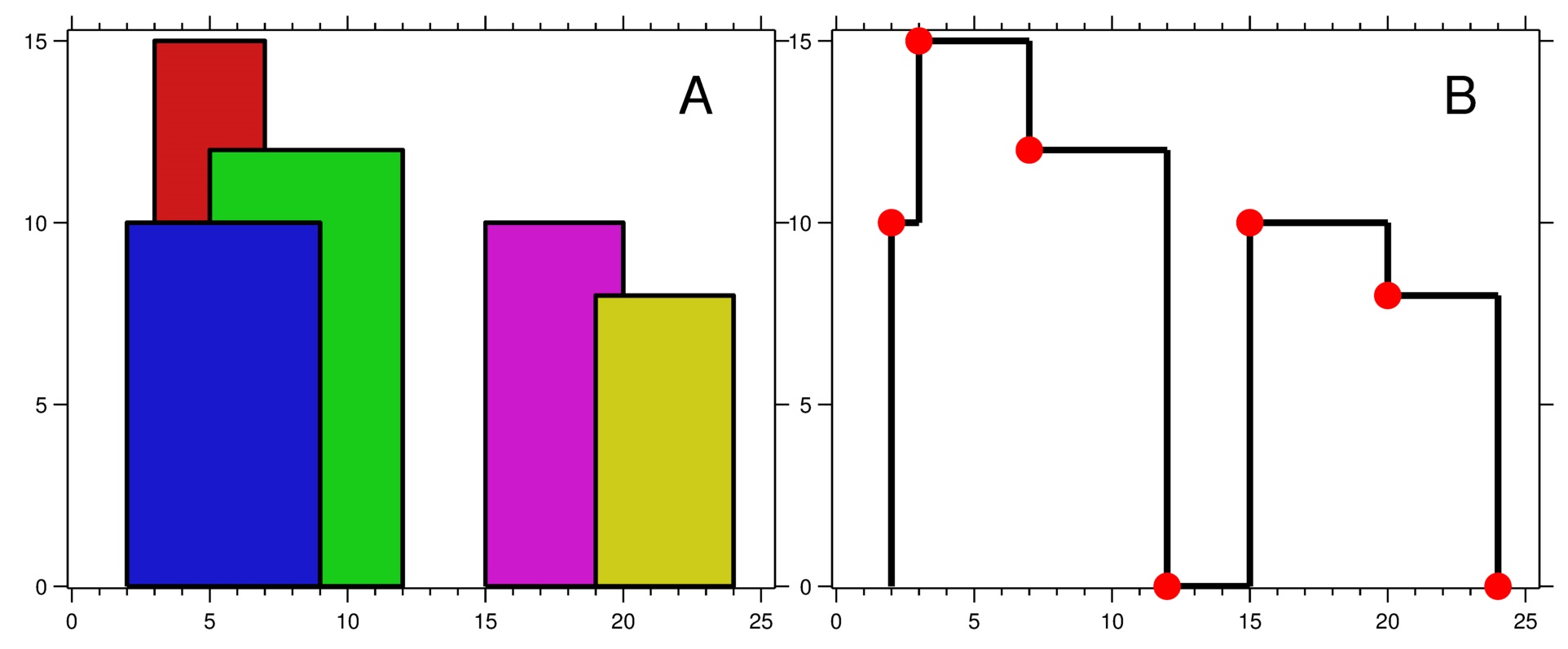
Input: buildings = [[2,9,10],[3,7,15],[5,12,12],[15,20,10],[19,24,8]]
Output: [[2,10],[3,15],[7,12],[12,0],[15,10],[20,8],[24,0]]
Explanation:
Figure A shows the buildings of the input.
Figure B shows the skyline formed by those buildings. The red points in figure B represent the key points in the output list.

Example 2:

Input: buildings = [[0,2,3],[2,5,3]]
Output: [[0,3],[5,0]]

Constraints: 1 <= buildings.length <= 10<sup>4</sup>
0 <= left<sub>i</sub> < right<sub>i</sub> <= 2<sup>31</sup> - 1 1 <= height<sub>i</sub> <= 2<sup>31</sup> - 1
* buildings is sorted by left<sub>i</sub> in non-decreasing order.

题目大意：

N/A

解题思路：

Heap(高度最大堆) + 端点排序法(先端点再高度逆序)
不是高频题，但思路值得学习
Heap(高度最大堆): LeetCode 253 Meeting Rooms II方法一，终点的最小堆
端点排序法(先端点再高度逆序)： LeetCode 253 Meeting Rooms II方法二
meeting room是新线段的start逼栈顶终点出堆，此题也是同样，但用高度的最大堆维护当前最高大厦，这与题意符合。

• 为什么要加入结束点?
  
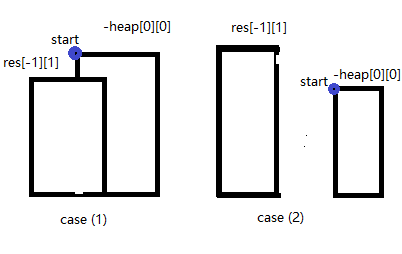
  两种情况，第一种情况没有问题，但第二种情况就会漏掉第一栋大厦的结束点。原因是出堆的点没有被处理，但出堆的点可能有多个而且若没有新大厦它不能出堆，所以结束点逼它出堆。

• 为什么高度逆序?
  
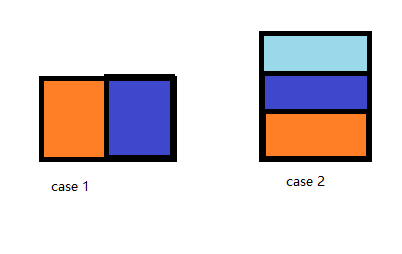
  第一种情况在坐标2这个位置有两节点(2, 0, 0)第一栋大厦结束点, (2, 5, 3)第二栋大厦开始点，若不按高度排序，第一栋结束点会逼第一栋开始点出堆，产生天际线。若按高度逆序，后者先入堆，第一栋开始点出堆也不会产生天际线。类似于heapq.heapreplace先加入再删除或者LeetCode 354 Russian Doll Envelopes的排序方式

解题步骤：

N/A

注意事项：

1. 先顺序排序端点再逆序高度，因为当结束点和始点重合时，让高度大的先入堆可以确保不会产生矮的天际线，否则这些矮的天际线实际被包含在高的大厦里。
2. 结束点也要加入循环但不入堆。这样产生两点：
   1) start >= heap[0][1]要取等号，否则不能让这栋大厦结束点出堆。
   2) 结束点不入堆，因为它只用于产生结束点从而加入到结果集，它不产生高度，只有产生高度的点才会被加入到堆
3. 与前高度不同，也就是高度发生变化就入堆
4. 确保res[-1][1] != -heap[0][0]。用只有一栋大厦作为test case。
   1) 因为用到了res[-1][1]，所以res初始化加入[-float(‘inf’), 0]，第一个值不会用到所以无所谓不妨去负无穷，高度为0；
   2) 最后结果要排除这个点，取res[1:]
   3) 因为要用到heap[0][0]，也就是heap要永远有节点。初始化加入[0, float(‘inf’)]，高度为0，用于产生在地平线的点的高度，结束点为无穷大，确保不会被逼出堆。
   总结加入res中的为起始点，加入heap中的为结束点，它们高度均为0，但端点对称分别为负正无穷。

大厦题，首尾加入节点：
LeetCode 084 Largest Rectangle in Histogram
LeetCode 218 The Skyline Problem

实现上有点似：
LeetCode 239 Sliding Window Maximum 模板，计算，排除
LeetCode 218 The Skyline Problem 模板，加入，计算

Python代码：

def getSkyline(self, buildings: List[List[int]]) -> List[List[int]]:
	events = sorted(buildings + [[end, 0, 0] for _, end, _ in buildings], key=lambda x: (x[0], -x[2]))
	heap, res = [(0, float('inf'))], [[-float('inf'), 0]]
	for start, end, height in events:
		while heap and start >= heap[0][1]:
			heapq.heappop(heap)
		if height > 0: # don't push ends into the heap
			heapq.heappush(heap, (-height, end))
		if res[-1][1] != -heap[0][0]:
			res.append([start, -heap[0][0]])
	return res[1:]

算法分析：

时间复杂度为O(nlogn)，空间复杂度O(k), k为重合天际线个数，此复杂度跟Meeting Rooms II一致