LeetCode 142 Linked List Cycle II

LeetCode

Given the head of a linked list, return the node where the cycle begins. If there is no cycle, return null.

There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the next pointer. Internally, pos is used to denote the index of the node that tail’s next pointer is connected to (0-indexed). It is -1 if there is no cycle. Note that pos is not passed as a parameter.

Do not modify the linked list.

Example 1:

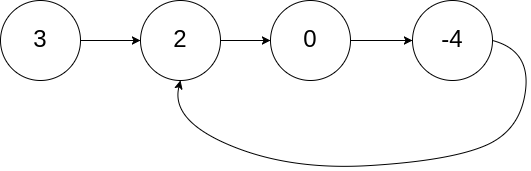
Input: head = [3,2,0,-4], pos = 1
Output: tail connects to node index 1
Explanation: There is a cycle in the linked list, where tail connects to the second node.

Example 2:

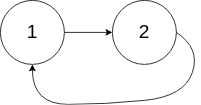
Input: head = [1,2], pos = 0
Output: tail connects to node index 0
Explanation: There is a cycle in the linked list, where tail connects to the first node.

Example 3:

Input: head = [1], pos = -1
Output: no cycle
Explanation: There is no cycle in the linked list.

Constraints:

The number of the nodes in the list is in the range [0, 10<sup>4</sup>]. -10<sup>5</sup> <= Node.val <= 10<sup>5</sup>
pos is -1 or a valid index in the linked-list.

*Follow up: Can you solve it using O(1) (i.e. constant) memory?

题目大意：

求LL是否存在循环，若存在返回循环起点

解题思路：

先用快慢指针找到相遇点，然后将slow指针移回fake_head起点，同速度移动直到相遇即为所求

证明：

A为起点，B为快慢指针相遇点，假设长度分别为z, y, x

fast在相遇时走过的距离为: z + x + y + y, 比slow多走一圈  
slow在相遇时走过的距离为: z + y  
由于fast速度是slow的两倍，所以相遇时，同一时间内，走过的距离也是两倍。
z + x + y + y = 2 * (z + y)
x = z得证

解题步骤：

N/A

注意事项：

1. 不涉及删除，所以不需要哟用到fake_node，但循环中先走再判断。
2. 循环可能不存在，此时返回None

Python代码：

def detectCycle(self, head: ListNode) -> ListNode:
	fast, slow= head, head
	while fast and fast.next:
		fast, slow = fast.next.next, slow.next
		if fast == slow: # meets again
			break
	if not fast or not fast.next:
		return None # remember
	slow = head
	while fast != slow:
		fast, slow = fast.next, slow.next
	return fast

算法分析：

时间复杂度为O(n)，空间复杂度O(1)