LeetCode 289 Game of Life

LeetCode

According to Wikipedia’s article: “The Game of Life, also known simply as Life, is a cellular automaton devised by the British mathematician John Horton Conway in 1970.”

The board is made up of an m x n grid of cells, where each cell has an initial state: live (represented by a 1) or dead (represented by a 0). Each cell interacts with its eight neighbors (horizontal, vertical, diagonal) using the following four rules (taken from the above Wikipedia article):

1. Any live cell with fewer than two live neighbors dies as if caused by under-population.
2. Any live cell with two or three live neighbors lives on to the next generation.
3. Any live cell with more than three live neighbors dies, as if by over-population.
4. Any dead cell with exactly three live neighbors becomes a live cell, as if by reproduction.

The next state is created by applying the above rules simultaneously to every cell in the current state, where births and deaths occur simultaneously. Given the current state of the m x n grid board, return the next state.

Example 1:

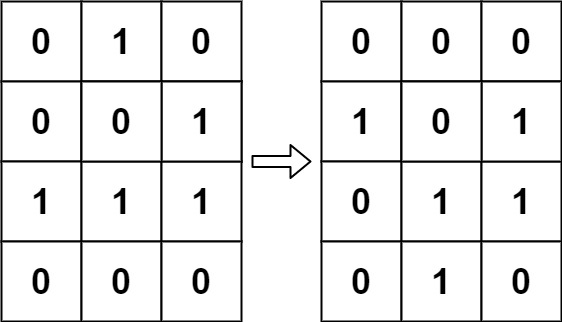
Input: board = [[0,1,0],[0,0,1],[1,1,1],[0,0,0]]
Output: [[0,0,0],[1,0,1],[0,1,1],[0,1,0]]

Example 2:

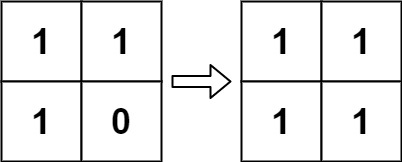
Input: board = [[1,1],[1,0]]
Output: [[1,1],[1,1]]

Constraints:

m == board.length n == board[i].length
1 <= m, n <= 25 board[i][j] is 0 or 1.

Follow up:

Could you solve it in-place? Remember that the board needs to be updated simultaneously: You cannot update some cells first and then use their updated values to update other cells. In this question, we represent the board using a 2D array. In principle, the board is infinite, which would cause problems when the active area encroaches upon the border of the array (i.e., live cells reach the border). How would you address these problems?

题目大意：

根据临近8个细胞的情况来决定生死。若该细胞是live和临近有2-3个是live，仍然live。若该细胞是dead和临近有3个是live，复生。其他都变成dead

解题思路：

N/A

解题步骤：

N/A

注意事项：

board[:] = res赋值到原数组一定要用冒号

Python代码：

OFFSETS = [(-1, -1), (-1, 0), (-1, 1), (0, -1), (0, 1), (1, -1), (1, 0), (1, 1)]
class Solution(TestCases):

    def gameOfLife(self, board: List[List[int]]) -> None:
        res = [[0 for _ in range(len(board[0]))] for _ in range(len(board))]
        for i in range(len(board)):
            for j in range(len(board[0])):
                live_neighbor_num = self.get_live_neighbor_num(board, i, j)
                if board[i][j] == 0 and live_neighbor_num == 3:
                    res[i][j] = 1
                if board[i][j] == 1 and live_neighbor_num in [2, 3]:
                    res[i][j] = 1
        board[:] = res

    def get_live_neighbor_num(self, board, i, j):
        res = 0
        for _dx, _dy in OFFSETS:
            x, y = i + _dx, j + _dy
            if 0 <= x < len(board) and 0 <= y < len(board[0]) and board[x][y] == 1:
                res += 1
        return res

算法分析：

时间复杂度为O(8n²)，空间复杂度O(n²)

算法II解题思路O(1) Space：

用一个数字来记录前后状态，2表示从0到1,3表示从1到0

注意事项：

不同之处有两个： Line 11不再是board[i][j]为1的情况，而是从1变成0的情况： live_neighbor_num not in [2, 3]
最后扫一遍矩阵，将2和3变回1和0
board[i][j] == 0和board[i][j] == 1不用改，因为从左到有从上到下扫描，到该格时，该格的值并未变，只能是0或1，它的左和上3邻居才变了。

Python代码：

OFFSETS = [(-1, -1), (-1, 0), (-1, 1), (0, -1), (0, 1), (1, -1), (1, 0), (1, 1)]
class Solution(TestCases):

     def gameOfLife2(self, board: List[List[int]]) -> None:
        # STATUS = {2: (0, 1), 3: (1, 0)}
        for i in range(len(board)):
            for j in range(len(board[0])):
                live_neighbor_num = self.get_live_neighbor_num2(board, i, j)
                if board[i][j] == 0 and live_neighbor_num == 3:
                    board[i][j] = 2
                if board[i][j] == 1 and live_neighbor_num not in [2, 3]:
                    board[i][j] = 3
        for i in range(len(board)):
            for j in range(len(board[0])):
                if board[i][j] == 2:
                    board[i][j] = 1
                if board[i][j] == 3:
                    board[i][j] = 0

    def get_live_neighbor_num2(self, board, i, j):
        res = 0
        for _dx, _dy in OFFSETS:
            x, y = i + _dx, j + _dy
            if 0 <= x < len(board) and 0 <= y < len(board[0]) and board[x][y] in [1, 3]:
                res += 1
        return res

算法分析：

时间复杂度为O(8n²)，空间复杂度O(1)

算法III解题思路

另外一条follow up是如果matrix无界，可以假设大部分是死细胞，先收集live细胞的list，然后计算live细胞的临近细胞即可