KK's blog

每天积累多一些

0%

LeetCode 973 K Closest Points to Origin

Posted on Edited on Disqus:

LeetCode



Given an array of points where points[i] = [x<sub>i</sub>, y<sub>i</sub>] represents a point on the X-Y plane and an integer k, return the k closest points to the origin (0, 0).

The distance between two points on the X-Y plane is the Euclidean distance (i.e., √(x<sub>1</sub> - x<sub>2</sub>)<sup>2</sup> + (y<sub>1</sub> - y<sub>2</sub>)<sup>2</sup>).

You may return the answer in any order. The answer is guaranteed to be unique (except for the order that it is in).

Example 1:



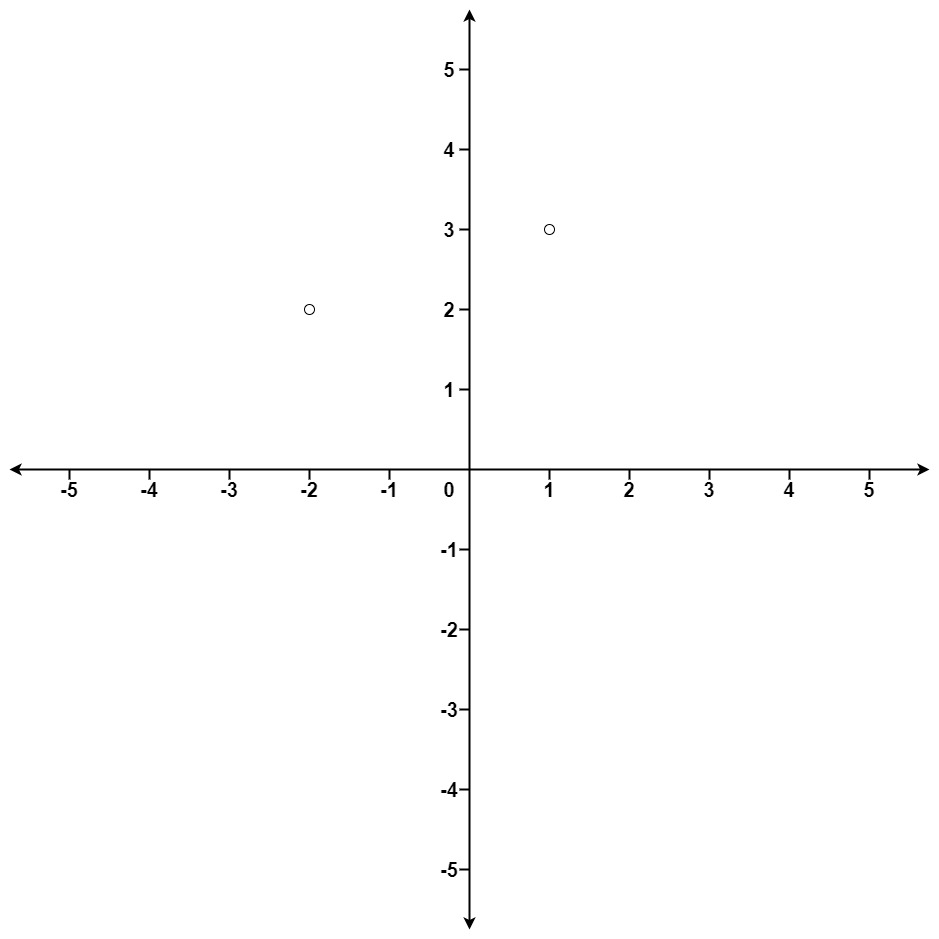
Input: points = [[1,3],[-2,2]], k = 1
Output: [[-2,2]]
Explanation:
The distance between (1, 3) and the origin is sqrt(10).
The distance between (-2, 2) and the origin is sqrt(8).
Since sqrt(8) < sqrt(10), (-2, 2) is closer to the origin.
We only want the closest k = 1 points from the origin, so the answer is just [[-2,2]].


Example 2:

Input: points = [[3,3],[5,-1],[-2,4]], k = 2
Output: [[3,3],[-2,4]]
Explanation: The answer [[-2,4],[3,3]] would also be accepted.


Constraints:

1 <= k <= points.length <= 10<sup>4</sup> -10<sup>4</sup> < x<sub>i</sub>, y<sub>i</sub> < 10<sup>4</sup>

算法思路：

最大堆

注意事项：

  1. 求最小距离用最大堆，距离的相反数入堆
  2. 与堆顶比较，跟模板一样仍然是大于号

Python代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def kClosest(self, points: List[List[int]], k: int) -> List[List[int]]:
	if not points or not points[0]:
		return 0
	heap, res = [], []
	for i in range(len(points)):
		x, y = points[i][0], points[i][1] # x=-2, y=2
		if i < k: # i=1, k=1
			heapq.heappush(heap, (-(x * x + y * y), x, y)) # -10, 1, 3
		elif -(x * x + y * y) > heap[0][0]: # -8 > -10
			heapq.heapreplace(heap, (-(x * x + y * y), x, y)) # -8, -2, -2

	while heap:
		(dis, x, y) = heapq.heappop(heap) # -8, -2, -2
		res.append([x, y])
	return res

Java代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
public int[][] kClosest(int[][] points, int K) {
	PriorityQueue<Point> maxHeap = new PriorityQueue<Point>(K,
			new Comparator<Point>() {
				@Override
				public int compare(Point o1, Point o2) {
					return distance(o2, o1); // descending
				}
			}
	);
	
	for(int i = 0; i < points.length; i++) {
		Point p = new Point(points[i][0], points[i][1]);
		if(maxHeap.size() < K)
			maxHeap.offer(p);
		else if(distance(p, maxHeap.peek()) < 0) {
			maxHeap.poll();
			maxHeap.offer(p);
		}
	}
	int[][] res = new int[K][2];
	int j = 0;
	while(!maxHeap.isEmpty()) {
		Point p = maxHeap.poll();
		res[j][0] = p.x;
		res[j][1] = p.y;
		j++;
	}
	return res;
}

int distance(Point o1, Point o2) {
	return (o1.x * o1.x + o1.y * o1.y) - (o2.x * o2.x + o2.y * o2.y);
}

class Point {
	 int x;
	 int y;
	 Point() { x = 0; y = 0; }
	 Point(int a, int b) { x = a; y = b; }
}

算法分析：

时间复杂度为O(nlogk)，空间复杂度O(k)

Free mock interview