KK's blog

每天积累多一些

0%

LeetCode 212 Word Search II

Posted on Edited on Disqus:

LeetCode



Given an m x n board of characters and a list of strings words, return all words on the board.

Each word must be constructed from letters of sequentially adjacent cells, where adjacent cells are horizontally or vertically neighboring. The same letter cell may not be used more than once in a word.

Example 1:



Input: board = [[“o”,”a”,”a”,”n”],[“e”,”t”,”a”,”e”],[“i”,”h”,”k”,”r”],[“i”,”f”,”l”,”v”]], words = [“oath”,”pea”,”eat”,”rain”]
Output: [“eat”,”oath”]


Example 2:



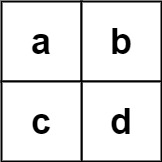
Input: board = [[“a”,”b”],[“c”,”d”]], words = [“abcb”]
Output: []


Constraints:

m == board.length n == board[i].length
1 <= m, n <= 12 board[i][j] is a lowercase English letter.
`1 <= words.length <= 3 104*1 <= words[i].length <= 10*words[i]consists of lowercase English letters. * All the strings ofwords` are unique.

算法思路：

N/A

注意事项：

  1. 用Trie来保存单词列表，这样每次DFS的每一步都可以O(1)时间知道是否和单词吻合，而不是O(n)
  2. 难点1: Trie的接口有startswith, search, insert，仅insert可以用，其他两个不支持与DFS同步搜索。所以要写一个新函数：其实修改startsWith将for循环去掉当然DFS的API也要改，去掉word, word_index加入trie, trie_node, path, res
  3. TLE错误，因为比如矩阵为[abc]，单词列表为abc, abc, abc，这样abc加入到结果后就不应该再搜abc，因为结果不能重且效率大打折扣。如果找到了单词，就应该将它从Trie中去掉，避免无谓的搜索，条件是该节点children长度为0，就父节点就将key删除。如果还有儿子节点只能标记is_end为False。Line 29 - 31和35 - 36

Python代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
OFFSETS = [(0, 1), (1, 0), (-1, 0), (0, -1)]
class Solution(TestCases):

    def findWords(self, board: List[List[str]], words: List[str]) -> List[str]:
        if not board or not board[0] or not words:
            return []
        trie, res = Trie(), []
        for word in words:
            trie.insert(word)

        visited = [[False for _ in range(len(board[0]))] for _ in range(len(board))]
        for i in range(len(board)):
            for j in range(len(board[0])):
                self.dfs(board, i, j, visited, trie, trie.get_head(), '', res)
        return list(res)

    def dfs(self, board, start_x, start_y, visited, trie, trie_node, path, res):
        if start_x < 0 or start_x >= len(board) or start_y < 0 or start_y >= len(board[0]):
            return
        if visited[start_x][start_y]:
            return
        trie_child = trie.search_one_node(board[start_x][start_y], trie_node)
        if not trie_child:
            return
        visited[start_x][start_y] = True
        path += board[start_x][start_y]
        if trie_child.is_end:
            res.append(path)
            trie_child.is_end = False
            if len(trie_child.children) == 0 and board[start_x][start_y] in trie_node.children:
                trie_node.children.pop(board[start_x][start_y])
        for dx, dy in OFFSETS:
            self.dfs(board, start_x + dx, start_y + dy, visited, trie, trie_child, path, res)
        path = path[:-1]
        visited[start_x][start_y] = False
        if len(trie_child.children) == 0 and board[start_x][start_y] in trie_node.children:
            trie_node.children.pop(board[start_x][start_y])


class Trie:
    def __init__(self):
        self.head = TrieNode()

    def insert(self, word: str) -> None:
        if not word:
            return
        it = self.head
        for i in range(len(word)):
            it = it.children[word[i]]
        it.is_end = True

    def search_one_node(self, c: str, trie_node):
        if c not in trie_node.children:
            return None
        else:
            return trie_node.children[c]

class TrieNode:

    def __init__(self):
        self.children = collections.defaultdict(TrieNode)  # {}
        self.is_end = False

上述代码比较复杂，可以先写这个LTE版本, 它在最后结果去重，但是对于重复单词会LTE，如[‘a’, … ‘a’]. 所以演变成最优版本，需要删除Trie的节点

Python代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
def findWords(self, board: List[List[str]], words: List[str]) -> List[str]:
	...
	return list(set(res))

def dfs(self, board, start_x, start_y, visited, trie, trie_node, path, res):
	if start_x < 0 or start_x >= len(board) or start_y < 0 or start_y >= len(board[0]):
		return
	if visited[start_x][start_y]:
		return
	trie_child = trie.search_one_node(board[start_x][start_y], trie_node)
	if not trie_child:
		return
	visited[start_x][start_y] = True
	path += board[start_x][start_y]
	if trie_child.is_end:
		res.append(path)
	for dx, dy in OFFSETS:
		self.dfs(board, start_x + dx, start_y + dy, visited, trie, trie_child, path, res)
	path = path[:-1]
	visited[start_x][start_y] = False

算法分析：

时间复杂度为O(n2*4*3L-1)，空间复杂度O(n2), n是矩阵长度，L是最大单词长度.
3是因为访问过的节点不合法，也就是来的节点不能再走一次，所以只能3个方向,第一个可以4个方向，其他步是3个方向

有一个方法是不用Trie而是将单词所有prefix放入到set中，但会TLE，因为时间复杂度为O(n23n*n)，它不会剪枝，从顶点出发，最差情况是z型走完board，此时路径长度为n*n.

Free mock interview