LeetCode 133 Clone Graph

LeetCode 133 Clone Graph

Given a reference of a node in a connected#Connected_graph) undirected graph.

Return a deep copy (clone) of the graph.

Each node in the graph contains a val (int) and a list (List[Node]) of its neighbors.

class Node {
    public int val;
    public List neighbors;
}

Test case format:

For simplicity sake, each node’s value is the same as the node’s index (1-indexed). For example, the first node with val = 1, the second node with val = 2, and so on. The graph is represented in the test case using an adjacency list.

Adjacency list is a collection of unordered lists used to represent a finite graph. Each list describes the set of neighbors of a node in the graph.

The given node will always be the first node with val = 1. You must return the copy of the given node as a reference to the cloned graph.

Example 1:

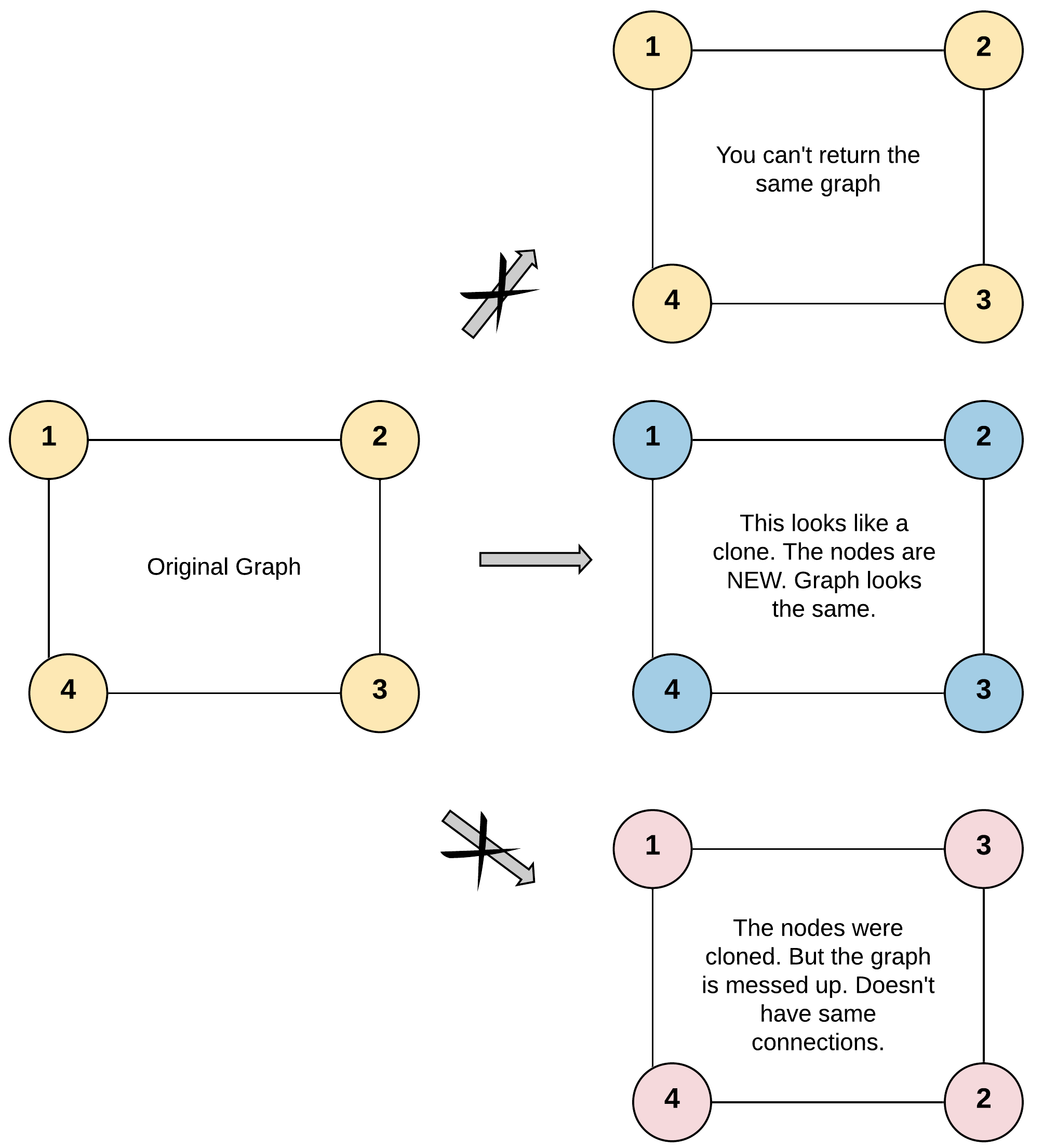
**Input:** adjList = [[2,4],[1,3],[2,4],[1,3]]
**Output:** [[2,4],[1,3],[2,4],[1,3]]
**Explanation:** There are 4 nodes in the graph.
1st node (val = 1)'s neighbors are 2nd node (val = 2) and 4th node (val = 4).
2nd node (val = 2)'s neighbors are 1st node (val = 1) and 3rd node (val = 3).
3rd node (val = 3)'s neighbors are 2nd node (val = 2) and 4th node (val = 4).
4th node (val = 4)'s neighbors are 1st node (val = 1) and 3rd node (val = 3).

Example 2:

**Input:** adjList = [[]]
**Output:** [[]]
**Explanation:** Note that the input contains one empty list. The graph consists of only one node with val = 1 and it does not have any neighbors.

Example 3:

**Input:** adjList = []
**Output:** []
**Explanation:** This an empty graph, it does not have any nodes.

Example 4:

**Input:** adjList = [[2],[1]]
**Output:** [[2],[1]]

Constraints:

• 1 <= Node.val <= 100
• Node.val is unique for each node.
• Number of Nodes will not exceed 100.
• There is no repeated edges and no self-loops in the graph.
• The Graph is connected and all nodes can be visited starting from the given node.

题目大意：

深度复制图。注意要复制所有邻接节点。

算法I解题思路(推荐)：

三步走。分开写逻辑会显得清晰点。

1. BFS搜索所有节点，变成邻接表节点列表。
2. 复制节点。旧新节点映射存在dict中
3. 根据node.neighbors复制边。

注意事项：

1. 空节点判断Line 2-3
2. BFS访问是收集节点列表，并不是变成邻接表。如果是含循环的图，由于用了visited，所以邻接表只能复制一半的边，不能用邻接表

Python代码：

def cloneGraph(self, node: 'Node') -> 'Node':
	if not node:
		return None
	di = {}
	node_list = self.bfs(node)
	for n in node_list:
		di[n] = Node(n.val)
	for n in node_list:
		for n2 in n.neighbors:
			di[n].neighbors.append(di[n2])
	return di[node]

def bfs(self, input):
	queue = deque([input])
	visited = {input}
	# graph = collections.defaultdict(list)
	res = []
	while queue:
		node = queue.popleft()
		# graph[node] = []
		res.append(node)
		for neighbor in node.neighbors:
			if neighbor in visited:
				continue
			queue.append(neighbor)
			visited.add(neighbor)
			# graph[node].append(neighbor)
	return res

Java代码：

// another bfs3 method uses 3 steps, convert graph to adjacent list by bfs (flatten the graph), 
//clone vertices, clone edges
public void bfs3(UndirectedGraphNode node, HashMap<UndirectedGraphNode, UndirectedGraphNode> map) {
	ArrayList<UndirectedGraphNode> nodes = getNodes(node);
	
	// Copy vertices
	for(UndirectedGraphNode old : nodes) {
		UndirectedGraphNode newNode = new UndirectedGraphNode(old.label);
		map.put(old, newNode);
	}
	
	// Copy edges
	for(UndirectedGraphNode old : nodes) {
		for(UndirectedGraphNode neighbor : old.neighbors) {
			map.get(old).neighbors.add(map.get(neighbor));
		}
	}
}

public ArrayList<UndirectedGraphNode> getNodes(UndirectedGraphNode node) {
	Queue<UndirectedGraphNode> q = new LinkedList<>();
	Set<UndirectedGraphNode> result = new HashSet<>();
	q.offer(node);
	result.add(node); // Use result set so we can save the visited set
	while(!q.isEmpty()) {
		UndirectedGraphNode n = q.poll();
		for(UndirectedGraphNode neighbor : n.neighbors) {
			if(result.contains(neighbor))
				continue;
			q.offer(neighbor);
			result.add(neighbor);
		}
	}
	ArrayList<UndirectedGraphNode> reList = new ArrayList<UndirectedGraphNode>();
	reList.addAll(result);
	return reList;
}

---

算法II解题思路：

不分开三步写

Java代码：

public UndirectedGraphNode cloneGraph2(UndirectedGraphNode node) {
	if(node == null)
		return null;
	
	HashMap<UndirectedGraphNode, UndirectedGraphNode> map = new HashMap<>();
	bfs(node, map);
	return map.get(node);
}

public void bfs(UndirectedGraphNode node, HashMap<UndirectedGraphNode, UndirectedGraphNode> map) {
	Queue<UndirectedGraphNode> q = new LinkedList<>();
	q.offer(node);
	map.put(node, new UndirectedGraphNode(node.label));
	while(!q.isEmpty()) {
		UndirectedGraphNode head = q.poll();
		for(UndirectedGraphNode neighbor : head.neighbors) {
			if(!map.containsKey(neighbor)) {
				q.offer(neighbor);
				// Clone children's vertex
				map.put(neighbor, new UndirectedGraphNode(neighbor.label));
			}
			// Clone edge
			map.get(head).neighbors.add(map.get(neighbor));
		}
	}
}

---

算法II解题思路：

DFS。

public UndirectedGraphNode cloneGraph(UndirectedGraphNode node) {
	HashMap<Integer, UndirectedGraphNode> map = new HashMap<Integer, UndirectedGraphNode>();
	return cloneGraphR(node, map);
}

public UndirectedGraphNode cloneGraphR(UndirectedGraphNode node,
		HashMap<Integer, UndirectedGraphNode> map) {
	if (node == null)
		return node;
	if (map.containsKey(node.label))
		return map.get(node.label);

	UndirectedGraphNode result = new UndirectedGraphNode(node.label);
	map.put(node.label, result);
	for (UndirectedGraphNode child : node.neighbors) {
		result.neighbors.add(cloneGraphR(child, map));
	}
	return result;
}

算法分析：

时间复杂度为O(# of results)，空间复杂度O(lengh(high))。