KK's blog

每天积累多一些

0%

LeetCode 042 Trapping Rain Water

Posted on Edited on Disqus:

LeetCode 042 Trapping Rain Water

Given n non-negative integers representing an elevation map where the width of each bar is 1, compute how much water it is able to trap after raining.


The above elevation map is represented by array [0,1,0,2,1,0,1,3,2,1,2,1]. In this case, 6 units of rain water (blue section) are being trapped. Thanks Marcos for contributing this image!

Example:

**Input:** [0,1,0,2,1,0,1,3,2,1,2,1]
**Output:** 6

题目大意：

给出 n 个非负整数，代表一张X轴上每个区域宽度为 1 的海拔图, 计算这个海拔图最多能接住多少（面积）雨水。

解题思路：

画图解题。
比较直观的方法是找低谷，只有低谷才可以藏水。用一个递减栈来存所有呈递减趋势的下标，而当上升时就计算藏水量。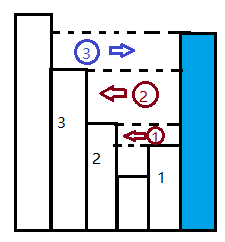

从图可以看出，栈中有最高的，3,2,1，最矮的已经出栈了。蓝色的bar准备入栈。计算水量是水平计算的。具体而言，
右边界是确定的，左边界以及高度都是由此bar相邻的在栈中的bar确定的。如1的水量由bar2的高度和位置确定。
同理bar2的水量由bar3确定。实质上，是求出栈的元素之间的水量，既然是之间，最后一个出栈就要特殊处理，需要准入栈
元素来确定。特殊之处是计算栈中最后一个将要被新bar踢出栈的bar3时，并没有相邻的bar作参考，
导致它需要用新bar作为参考，所以它不能在while中处理，需要特别处理，主要因为它是最后一个，属于edge case。

解题步骤：

  1. 遍历数组
  2. 若比上一个高度递增，出栈直至栈中下标对应高度大于当前高度（保持递减栈）。每次出栈，用上一轮的高度作为底部计算高度差
    乘以下标距离即为横向藏水增量，更新底部进入下一次出栈。
  3. 出栈完成后，根据新bar计算最后一个bar的水量，用当前高度计算藏水增量。
  4. 加入下标到栈中

公式：

1
水量 = 准入栈下标与相邻栈(栈顶)的下标i - stack[-1] - 1 乘以 (相邻栈高度 - 刚出栈高度)

注意事项：

  1. [公式]水量 = 准入栈下标与相邻栈(栈顶)的下标i - stack[-1] - 1 乘以 (相邻栈高度 - 刚出栈高度)
    水量的宽度并不是用刚出栈的下标，因为如上图，2-3之间可能实际上不相邻（有些高度已出栈），若用当前栈的下标会忽略了2-3之间的水量。
  2. 最后一个出栈的宽度计算要还有相邻栈(栈顶)i - stack[-1] - 1才计算也就是栈不为空if stack。
  3. 最后一个出栈的高度公式要改成相邻栈高度 -> 准入栈高度。

Python代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
def trap(self, height: List[int]) -> int:
	stack = []
	sum = 0
	for i in range(len(height)):
		j = -1
		while stack and height[i] > height[stack[-1]]:
			j = stack.pop()
			if stack and height[i] > height[stack[-1]]:
				sum += (height[stack[-1]] - height[j]) * (i - stack[-1] - 1) # stack[-1] is the neighboring index
		if stack and j > 0:
			sum += (height[i] - height[j]) * (i - stack[-1] - 1)
		stack.append(i)
	return sum

算法分析：

时间复杂度为O(n)，空间复杂度O(n)。

算法II解题思路(推荐)：

算法I主要从面考虑，现在我们从点来考虑。下标4的水量取决于向左最大值（下标0）和向右最大值（下标12）中的较小值。
问题转化为求每个点的向左向右最大值。数组从左到右扫描，把当前最大值存入leftHeight中，这是向左最大值。

同理，数组从又到左扫描，得到向右最大值。对每个点取向左向右最大值的较小者，从而计算水量。此法实现起来简单很多。

Python代码：

1
2
3
4
5
6
7
8
9
10
11
def trap(self, height: List[int]) -> int:
	max_height = max(height)
	max_index = height.index(max_height)
	sum, left_max, right_max = 0, 0, 0
	for i in range(max_index):
		sum += max(0, left_max - height[i])
		left_max = max(left_max, height[i])
	for i in range(len(height) - 1, max_index, -1):
		sum += max(0, right_max - height[i])
		right_max = max(right_max, height[i])
	return sum

算法分析：

时间复杂度为O(n)，空间复杂度O(1)。

Free mock interview