KK's blog

每天积累多一些

0%

Union Find

Posted on Edited on Disqus:

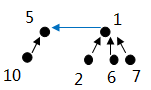
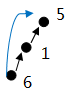
算法思路：

DFS用于需要知道具体路径的问题，而并查集方法用于不需知道具体路径只关心连通性的问题。
此算法把同一个连通集归结为同一个根节点，作为判断是否一个连通集的标识。它用深度为2的扁平树组织起来。这是查找操作。
另一个关键操作是联合两个不同连通集，就是直接把根节点直接作为另一课树的子节点。在这个过程中，新的树深度可能会大于2，但当要union路径大于2的节点是，会对其进行路径压缩。
最巧妙的操作当属find操作，将路径进行压缩，变成长度为1的路径，见步骤4。
可能有人会考虑用HashMap而不是树，HashMap查找也是很高效，但联合操作比较费时，因为要更新另一个树的所有节点的根节点。

算法步骤：

  1. 初始化UnionFind类，包括3个属性：count（独立连通数）, parent（某节点的父节点）, rank（连通集排名，只有每个连通集根节点的rank不为0，其他点均为0。这是一个描述连通集规模的变量，如果规模越大，
    rank值可能越大。合并时候，rank较小的话，规模也较小，这样用rank小的合并到rank大的，需要压缩路径的节点较少，复杂度更低）。合格的节点的parent初始化为自己的id，rank为0，count为所有合格节点数量。
  2. 遍历所有节点，union此节点及其相邻的节点（如上下左右）
  3. union时候，先find两节点的根节点，若相同忽略。若不同，合并此两连通集：rank大的连通集，作为rank小的连通集的父节点。若rank相等，选任一作为另一个的父节点且把它的rank加1。count减1。
    如下图，union 5和1的，find(6)会进行压缩路径，把6接到5下。
  4. find寻找根节点的同时，压缩成与根节点路径为1的连通。

例子矩阵：
{‘0’,’1’,’1’,’0’,’0’}
{‘1’,’1’,’1’,’0’,’0’}

应用条件：

动态计算连通数如305. Number of Islands II

注意事项：

  1. find中是if语句不是while语句，因为递归已经达到
  2. union中，是祖先节点相连，不是输入相连
  3. union的调用在类外面调用，不是在init里做

Python代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class UnionFind:

    def __init__(self, li):
        self.parent = collections.defaultdict(str)
        for s in li:
			self.parent[s] = s

    def find(self, s):
        if self.parent[s] != s:  # if statement
            self.parent[s] = self.find(self.parent[s])
        return self.parent[s]

    def union(self, s1, s2):
        root, root2 = self.find(s1), self.find(s2)
        if root != root2:
            self.parent[root] = root2 # remember not self.parent[s] = s2

注意事项：

find要注意压缩路径parent[i] = find(parent[i])

初始化：

1
2
3
4
5
6
7
8
9
10
class UnionFind {
	int[] parent;
	
	public Initialization(int n) {
        // initialize your data structure here.
        parent = new int[n + 1];
        for (int i = 1; i <= n; ++i)
            father[i] = i;
    }
}

查找：

1
2
3
4
5
6
public int find(int i) {
	if (parent[i] != i) {
		parent[i] = find(parent[i]); // path compression
	}
	return parent[i];
}

合并：

1
2
3
4
5
6
public void union(int a, int b) {
	int root_a = find(a);
	int root_b = find(b);
	if (root_a != root_b)
		parent[root_a] = root_b;
}

Java代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
class UnionFind {
	int count; // # of connected components
	int[] parent;
	int[] rank;

	public UnionFind(char[][] grid) { // for problem 200
		count = 0;
		int m = grid.length;
		int n = grid[0].length;
		parent = new int[m * n];
		rank = new int[m * n];
		for (int i = 0; i < m; ++i) {
			for (int j = 0; j < n; ++j) {
				if (grid[i][j] == '1') {
					parent[i * n + j] = i * n + j;
					++count;
				}
				rank[i * n + j] = 0;
			}
		}
	}

	public int find(int i) {
		if (parent[i] != i) {
			parent[i] = find(parent[i]); // path compression
		}
		return parent[i];
	}

	// union point x and y with rank
	public void union(int x, int y) {
		int rootx = find(x);
		int rooty = find(y);
		if (rootx != rooty) {
			if (rank[rootx] > rank[rooty]) {
				parent[rooty] = rootx;
			} else if (rank[rootx] < rank[rooty]) {
				parent[rootx] = rooty;
			} else {
				parent[rooty] = rootx;
				rank[rootx] += 1;
			}
			--count;
		}
	}

	public int getCount() {
		return count;
	}
}

public int numIslands3(char[][] grid) {
	if (grid == null || grid.length == 0) {
		return 0;
	}

	int nr = grid.length;
	int nc = grid[0].length;
	int num_islands = 0;
	UnionFind uf = new UnionFind(grid);
	for (int r = 0; r < nr; ++r) {
		for (int c = 0; c < nc; ++c) {
			if (grid[r][c] == '1') {
				grid[r][c] = '0';
				if (r - 1 >= 0 && grid[r - 1][c] == '1') {
					uf.union(r * nc + c, (r - 1) * nc + c);
				}
				if (r + 1 < nr && grid[r + 1][c] == '1') {
					uf.union(r * nc + c, (r + 1) * nc + c);
				}
				if (c - 1 >= 0 && grid[r][c - 1] == '1') {
					uf.union(r * nc + c, r * nc + c - 1);
				}
				if (c + 1 < nc && grid[r][c + 1] == '1') {
					uf.union(r * nc + c, r * nc + c + 1);
				}
			}
		}
	}

	return uf.getCount();
}

算法分析：

时间复杂度为O(MN)，空间复杂度O(MN)。M,N分别为矩阵长宽。遍历每个节点，而每个节点只会遍历4个相邻节点。

Ref：

并查集(Union-Find)算法介绍

Free mock interview