LeetCode 309 Best Time to Buy and Sell Stock with Cooldown

LeetCode 309 Best Time to Buy and Sell Stock with Cooldown

Say you have an array for which the i^th element is the price of a given stock on day i.

Design an algorithm to find the maximum profit. You may complete as many transactions as you like (ie, buy one and sell one share of the stock multiple times) with the following restrictions:

You may not engage in multiple transactions at the same time (ie, you must sell the stock before you buy again).
After you sell your stock, you cannot buy stock on next day. (ie, cooldown 1 day)

Example:

prices = [1, 2, 3, 0, 2]
maxProfit = 3
transactions = [buy, sell, cooldown, buy, sell]

题目大意：

给定一个数组，第i个元素代表某只股票在第i天的价格。设计一个算法计算最大收益。你可以完成多次交易（多次买入、卖出同一只股票），需要满足下列限制：
你不可以在同一时间参与多个交易（在买入股票之前必须卖出）。
在卖出股票之后，你不可以在第二天马上买入。（需要一天的冷却（CD）时间）。也就是卖出后过两天才能买入。

解题思路：

因为有限制条件，所以没有特别方法，只能计算所有结果，也就是用动态规划。动态规划首先是写出递归式（数学归纳法）。

定义f(n)为第n日卖出股票（一定要卖出，不能持有）的利润，加强了命题。
递归式如下图，f(n)只能由f(n-1)卖出后立刻买入（相当于n-1时候不卖出）或者f(n-3)卖出n-1时候买入两种情况。

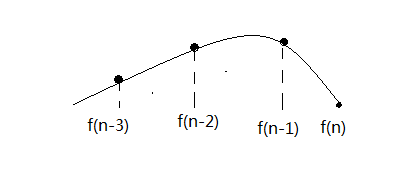
现在可以写出递归式：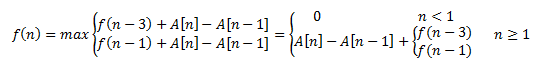

F(x)=max{f(1),…,f(n)}求加强命题最大值即为本题解。
这里考虑到负数，方便程序实现，否则，f(n)的前3个值计算就不能放入循环而要特别处理了。

注意事项：

数组为空或者1个
负数组的实现方法

Java代码：

public int maxProfit(int[] prices){
	int sell[] = new int[prices.length];
	int max = 0;
	for(int i=1;i<prices.length;i++){
		sell[i] = Math.max(f(i-3, sell), f(i-1, sell))+ prices[i]-prices[i-1];
		if(sell[i]>max)
			max = sell[i];
	}
	return max;		
}

public int f(int i, int[] r){
	if(i<1)
		return 0;
	else
		return r[i];

这个实现有个错误就是忽略了一种重要的情况：f(n-4),…,f(1)的情况。看以下例子：[6,1,6,4,3,0,2]

Index	0	1	2	3	4	5	6
price	6	1	6	4	3	0	2
f(n)	0	-5	5	3	2	2	5

按照上面算法结果为5，但是很容易看出来1->6, 0->2结果是7。问题出在最后一个f(6)=max{f(3),f(5)}+2=max{3,2}+2。很明显，第3天卖出获利为3并不是最佳，第二天卖出获利为5才是最佳，我们忽略了f(n-3)之前的所有情况。解决方案是再创建一个数组维护前n天最大获利值。
定义g(n)为第n日（包括第n日）前卖出股票（不一定要第n天卖出）的利润。修改递归式为，把f(n-3)改为g(n-3)：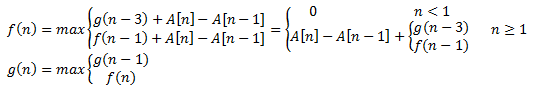

Java代码：

public int maxProfit2(int[] prices){
	int sell[] = new int[prices.length];
	int preSell[] = new int[prices.length];
	int max = 0;
	for(int i=1;i<prices.length;i++){
		sell[i] = Math.max(g(i-3, preSell), f(i-1, sell))+ prices[i]-prices[i-1];
		if(sell[i]>max)
			max = sell[i];
		
		preSell[i] = Math.max(preSell[i-1], sell[i]);
	}
	return max;		
}

public int f(int i, int[] r){
	if(i<1)
		return 0;
	else
		return r[i];
}

public int g(int i, int[] g){
	if(i<1)
		return 0;
	else
		return g[i];
}

算法分析：

时间复杂度为O(n)，n为数组长度，空间复杂度O(n)。

current, first分别通过f和g的计算公式计算，second是通过current获得

Python代码：

# g(n) = max{f(n), g(n-1)}
# f(n) = A[n] - A[n - 1] + max{f(n - 1), g(n-3)}
def maxProfit(self, prices: List[int]) -> int:
	# g(n-3), f(n-2), f(n-1)
	first, second, current = 0, 0, 0
	for i in range(1, len(prices)):
		current, second, first = prices[i] - prices[i - 1] + max(current, first), current, max(second, first)
	return max(current, second, first)

空间优化：

由于此题目，f(n)只与前三个状态有关f(n-1), f(n-2)(虽然没直接关系，但程序实现需要记录),g(n-3)。四个状态可以用三个变量
推进，如sell=Math.max(preSell, sell)，同一个变量旧状态更新到新状态，所以可以避免维护数组开销。
代入preSell=g(n-3), sell_1=f(n-2), sell=f(n-1)到公式即得
f(n) = sell = max{preSell, sell}+prices[n]-prices[i-1]
g(n-2) = preSell = max{g(n-3), f(n-2)} = max{preSell, sell_1}
f(n-1) = sell_1 = PreValue(sell)
本题解就是preSell, sell_1, sell的最大值。

Java代码：

public int maxProfit(int[] prices){
	//g(n-3), f(n-2), f(n-1)
	int preSell=0, sell_1=0, sell = 0;
	for(int i=1;i<prices.length;i++){
		int tmp = sell;
		sell = Math.max(preSell, sell)+ prices[i]-prices[i-1];
		preSell = Math.max(preSell, sell_1);
		sell_1 = tmp;
	}
	return Math.max(Math.max(preSell, sell_1), sell);		
}

算法分析：

时间复杂度为O(n)，n为数组长度，空间复杂度O(1)。本题有更简单解法但比较难想出。

最后注意事项：

数组为空或者1个
三种情况f(n-1),f(n-3),g(n-3)可以得到f(n)。解就是preSell, sell_1, sell的最大值。
DP流程，定义函数（是否加强）、递归式、空间优化。

KK's blog

LeetCode 309 Best Time to Buy and Sell Stock with Cooldown

题目大意：

解题思路：

注意事项：

Java代码：

Java代码：

算法分析：

Python代码：

空间优化：

Java代码：

算法分析：

最后注意事项：

相关题目：