KK's blog

每天积累多一些

0%

BFS

Posted on Edited on Disqus:

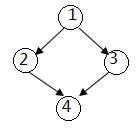
算法思路：

图用邻接表为输入，思路用Queue实现, 还要一个机制记录节点访问过没有，可以用HashSet，同时它作为结果存储BFS访问结果。
BFS多用于找最短路径
DFS多用于快速发现底部节点和具体路劲问题（如路径和或打印路径）。

BFS优缺点：
同一层的所有节点都会加入队列，所以耗用大量空间
仅能非递归实现
相比DFS较快，空间换时间
适合广度大的图
找环的话需要用拓扑排序

DFS优缺点：
无论是系统栈还是用户栈保存的节点数都只是树的深度，所以空间耗用小
有递归和非递归实现
由于有大量栈操作（特别是递归实现时候的系统调用），执行速度较BFS慢
适合深度大的图
找环的话比较容易实现

如果BFS和DFS都可以用，建议用BFS，因为工业应用中，BFS不用有限的栈空间，可以利用到所有内存。
BFS题目问自己是否需要按层遍历，是否需要visited

注意事项：

  1. 坐标型BFS，注意输入为(i, j)时候，x = node[0] + _dx[0], 用x不要用输入的i
  2. deque([(start[0], start[1])]), set([(startx, starty)])
  3. board[x][y] == ‘+’ 注意矩阵的其他不能遍历的元素，如L200中的0

其他:

  1. 只要把节点放入队列立即标记其为访问，不要在出列的时候才标记。否则同一个节点会入列多次。
    比如下图, 入列顺序为1,2,3,4,4。4入列了两次。
  2. 矩阵的遍历用方向List: OFFSETS = [(1, 0), (-1, 0), (0, 1), (0, -1)]

图遍历

只有是对所有节点BFS题型才需要将visited作为参数传入

Python代码：

1
2
3
4
5
6
7
8
9
10
11
12
def bfs(self, graph, start) -> List[int]:
	queue, res = deque([start]), []
	visited = set([start])
	while queue:
		node = queue.popleft()
		res.append(node)
		for neighbor in graph[node]:
			if neighbor in visited:
				continue
			queue.append(neighbor)
			visited.add(neighbor)
	return res

树模板只要把visited去掉，neighbor改成left和right

计算最短距离的图遍历(最常考的模板)

  • 只要加line 4和14
  • visited在函数内定义
  • 遇到target就返回最短距离，若离开循环返回-1，问清楚是否存在路径不存在的情况
  • 求距离公式不需要用min，因为这个遍历保证了最短距离了。 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def bfs_layer(self, graph, start) -> List[int]:
	queue = deque([start])
	visited = set([start])
	distance = {start: 1}
	while queue:
		node = queue.popleft()
		if node == target:
			return distance[node]
		for neighbor in graph[node]:
			if neighbor in visited:
				continue
			queue.append(neighbor)
			visited.add(neighbor)
			distance[neighbor] = distance[node] + 1
	return -1

按层遍历

核心是加这一行for _ in range(len(queue))
具体还要加line 5, 6和14, 15. 二叉树不需要visited。能用distance dict就尽量不用此法，因为多了一个循环。

注意事项：

  1. 关键行： 多这一行for循环 
1
2
3
4
5
6
7
8
9
10
11
12
13
def bfs_layer2(self, graph, visited, start) -> List[List[int]]:
	queue, res, layer = deque([start]), [], 0
	visited.add(start)
	while queue:
		for _ in range(len(queue)):
			node = queue.popleft()
			for neighbor in graph[node]:
				if neighbor in visited:
					continue
				queue.append(neighbor)
				visited.add(neighbor)
		layer += 1
	return res

Java代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
/*
 * graph: 邻接表
 * visited: 记录已访问节点，避免重复访问
 * start: BFS的根节点
 */
public void bfs(HashMap<Integer, LinkedList<Integer>> graph, HashSet<Integer> visited, int start){
	int num=0;
	Queue<Integer> q=new LinkedList<>();
	q.offer(start);
	visited.add(start);
	while(!q.isEmpty()){
		int node = q.poll();
		LinkedList<Integer> children = graph.get(node);
		for(int child : children){
			if (!visited.contains(child)){
				q.offer(child);
				visited.add(child);
			}
		}
	}
}

错误算法：

问题是加入到queue里面的child没有去重，这样容易queue爆炸式增长。

1
2
3
4
5
6
7
8
9
10
11
12
13
public void bfs(HashMap<Integer, LinkedList<Integer>> graph, HashSet<Integer> visited, int start){
	Queue<Integer> q=new LinkedList<>();
	q.offer(start);
	while(!q.isEmpty()){
		int node = q.poll();
		visited.add(node);
		LinkedList<Integer> children = graph.get(node);
		for(int child : children){
			if (!visited.contains(child))
				q.offer(child);
		}
	}
}

按层次遍历：

第一个思路是三重循环，先queue，然后该层所有节点，最后该层每一个节点的儿子。关键在于size = q.size();

Java代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
public void bfsByLayer3(HashMap<Integer, LinkedList<Integer>> graph, int start){
	Queue<Integer> q=new LinkedList<>();
	int layer = 1;
	q.offer(start);
	while(!q.isEmpty()){
		int size = q.size();
		for(int i = 0; i < size; i++) {// loop this layer
			int node = q.poll();
			System.out.println("node:"+node+" in layer "+ layer);
			LinkedList<Integer> children = graph.get(node);
			for(int child : children){// loop its children
				q.add(child);
			}
		}
		layer++;
	}
}

上述代码三重循环看似可读性不够好，所有可以用hashMap来记录每个点的距离从而减少第二重循环。
nodeToHeight.put(start, 1);
nodeToHeight.put(child, nodeToHeight.get(node) + 1);

Java代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
public void bfsByLayer4(HashMap<Integer, LinkedList<Integer>> graph, int start){
	Queue<Integer> q = new LinkedList<>();
	q.offer(start);
	Map<Integer, Integer> nodeToHeight = new HashMap<>();
	nodeToHeight.put(start, 1);
	while(!q.isEmpty()){

		int node = q.poll();
		System.out.println("node:"+node+" in layer "+ nodeToHeight.get(node));
		LinkedList<Integer> children = graph.get(node);
		for(int child : children){// loop its children
			q.add(child);
			nodeToHeight.put(child, nodeToHeight.get(node) + 1);
		}
		
	}
}

  1. q.isEmpty() && !q2.isEmpty()

第三思路是用两个队列来实现：用第一个队列存储该层的节点，第二个队列存储第一个队列中节点的儿子节点，
也就是下一次的节点。此思路比较容易实现。

Java代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
/* 假设不循环
 * graph: 邻接表
 * start: BFS的根节点
 */
public void bfsByLayer(HashMap<Integer, LinkedList<Integer>> graph, int start){
	Queue<Integer> q=new LinkedList<>();
	Queue<Integer> q2=new LinkedList<>();
	int layer = 1;
	q.offer(start);
	while(!q.isEmpty()){
		int node = q.poll();
		System.out.println("node:"+node+" in layer "+ layer);
		LinkedList<Integer> children = graph.get(node);
		for(int child : children){
			q2.offer(child);
		}
		if(q.isEmpty() && !q2.isEmpty()){
			q = q2;
			q2 = new LinkedList<>(); 
			layer++;
		}
	}
}

第四思路是只用一个队列来实现：层与层之间用结束符间隔，每遇到结束符，表示该层访问结束，下一层的节点也准备好
（不会再有新的节点加入到这一层），此时再往队列加入新的结束符。此思路对数据有一定限制，实现起来注意事项较多。

Java代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
public void bfsByLayer2(HashMap<Integer, LinkedList<Integer>> graph, int start){
	Queue<Integer> q=new LinkedList<>();
	int layer = 1;
	q.offer(start);
	q.offer(-1);
	while(!q.isEmpty()){
		int node = q.poll();
		if(node == -1){
			//确保有非结束符节点
			if(q.size()>0){
				q.offer(-1);
				layer++;
			}
			continue;
		}
		System.out.println("node:"+node+" in layer "+ layer);
		LinkedList<Integer> children = graph.get(node);
		for(int child : children){
			q.offer(child);
		}
	}
}

算法分析：

时间复杂度为O(n)，w为树的所有层里面的最大长度，空间复杂度O(w)。

Free mock interview